Jag tänkte på riskjusterad avkastning och kom slumpmässigt att tänka tillbaka på detta inlägg:
Och jag tänkte då på ett av problemen med sharpe:
Den säger ingenting om hur bra portföljen är på att faktiskt uppnå våra mål.
Säg t.ex att vi har en portfölj som ger 3% avkastning med nära noll volatilitet = våran sharpe är skyhög.
Men säg att vårat finansiella mål är 4% – våran portfölj är nästan garanterad att misslyckas med att uppfylla vårat mål!
Kan man då verkligen säga att en portfölj har skyhög riskjusterad avkastning om risken för misslyckande är skyhög? Så det ligger ju något i den gamla klyschan:
Man kan inte äta riskjusterad avkastning
Men det kan man ju lösa genom att lägga till hävstång på en portfölj med hög sharpe för att få upp förväntad absolutavkastning till något över vårat mål.
Och jag kom då också att tänka vad @zino, @robertk, mfl kom fram till angående sharpe och hävstång (tror det var det här ni kom fram till iaf):
Man kan inte höja sin sharpe genom att lägga till hävstång på portföljen (förutsatt att hävstången är dyrare än riskfria räntan)
Men om vi istället tänker på riskjusterad avkastning som hur bra portföljen är på att konsekvent uppfylla våra finansiella mål så har ju riskjusterade avkastningen definitivt gått upp med hävstång (utan hävstång var ju 3%-portföljen nästan garanterad att misslyckas även om sharpe var hög).
Annan liknelse: Risken att förlora pengar nominellt är teoretiskt noll när man lägger pengarna under sängen eller på ett bankkonto med 0% ränta. Men risken att förlora till inflationen är nära 100% över lång tid. Genom att investera i t.ex aktier så minskar vi risken att underprestera inflationen över lång tid jämfört med pengar under sängen, trots att aktier vanligtvis ses som mer riskfyllt än bankkonto.
Hemmasnickrade mått på riskjusterad avkastning
Det finns säkert redan akademiska svar på det här, men för skojs skull började jag bolla detta lite med chatgpt och vi kom fram till några alternativa mått på riskjusterad avkastning som tar vårat finansiella mål och våran individuella riskaptit i beaktande.
Den väsentliga skillnaden är att istället för att mäta avkastningen relativt till riskfria räntan så mäter man den relativt till ens finansiella mål.
Vanlig Sharpe = (Avkastning - Riskfria räntan) / Volatilitet
“Måljusterad Sharpe”: (Avkastning - Målavkastning) / Volatilitet
Och jag kom på att man kan göra ytterligare en justering av sharpe för att bestraffa volatilitet icke-linjärt och därmed simulera valfri riskaversion (volatilitetsaversion).
“Super-Sharpe” = Vanlig sharpe (eller måljusterad sharpe) * e^(-k * volatilitet)
Där k är våran volatilitetsaversion. k=0 är samma som vanlig sharpe. k>0 är större volatilitetsaversion.. K<0 är mindre volatilitetsaversion..
Ett annat alternativ som chatgpt föreslog var att räkna ut sannolikheten att portföljen uppnår sitt mål
För att räkna ut sannolikheten att portföljen lyckas/misslyckas ville chatgpt använda standardpoäng (z-score). Jag har aldrig använt z-score, men det verkar räknas ut så här:
Uträkning av z-score
Z-score: (Resultat - Medelvärde) / Standardavikelse
För vårat syfte: (Målavkastning - Förväntad avkastning) / Standardavikelse = z-score för att misslyckas slå målavkastningen
För att få z-score för att lyckas byter man bara tecken eller byter plats på målavkastning och förväntad avkastning i ekvationen.
Över flera samples n ska man tydligen kunna räkna ut det så här:
(Målvärdet - Medelvärdet) / (Standardavikelse / SQRT(n))
Z-score säger hur många standardavvikelser bort resultatet är från medelvärdet.
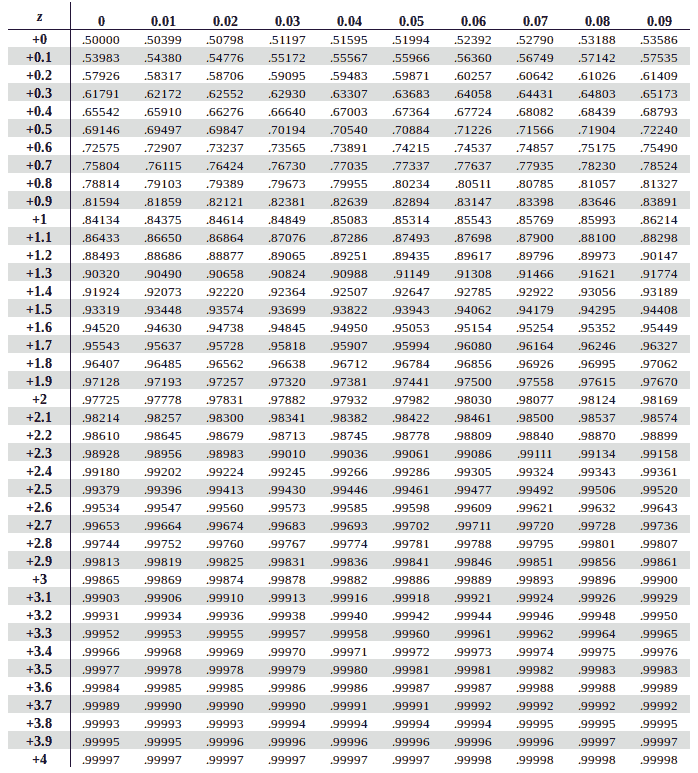
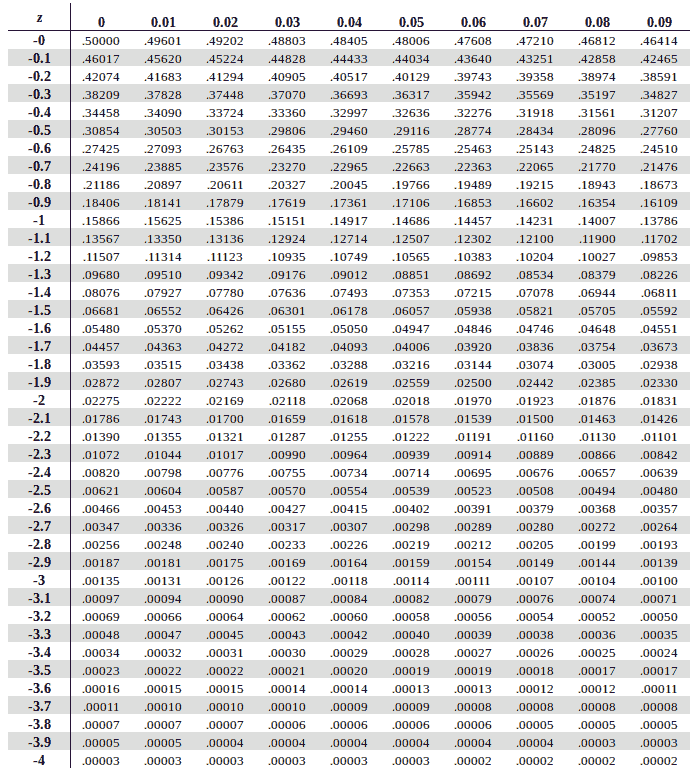
Och för att få fram sannolikheten så får man titta i en tabell för standardpoäng:
Z-score table
Referenser:
Exempel: Med ett finansiellt mål på 4%, en förväntad avkastning på 6% och 10% standardavikelse får vi denna z-score för att lyckas: (0,06-0,04) / 0,1 = 0,2
Z-score = 0,2 = 58% sannolikhet att lyckas över ett år
Över t.ex 20 år får vi då en z-score på: (0,06-0,04) / (0,1/SQRT(20)) = 0,89 = 81% att lyckas
(Notera att formeln för sharpe och z-score i grunden är densamma).
Om en global aktiefond har en sharpe (z-score) på 0,4 så innebär det att den statistiskt ska slå riskfria räntan runt 67% av åren.
En avancerad allvädersportfölj med en sharpe (z-score) på 1 ska innebära att den statistiskt slår riskfria räntan 85% av åren.
Hävstång: Rent hypotetiskt exempel
Grundavkastning: 6%
Riskfri ränta: 1%
Grundvolatilitet: 10%
Mål: 4%
Hävstång: Med hävstång så ökade jag volatiliteten med 1,5x/2x/3x, men avkastningen ökade jag bara med 1,3x/1,6x/1,9x.
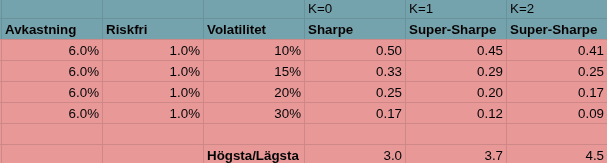
Först vanlig sharpe:
Som förväntat faller sharpe med hävstången. Super-sharpe faller ännu snabbare.
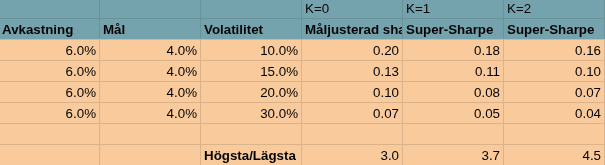
Sedan “måljusterad sharpe”:
Vi ser här att måljusterad sharpe stiger med hävstång upp till 2x! Men vid 3x sjunker den.
Men med måljusterad “super-sharpe” så börjar man också föredra låg eller ingen hävstång om man har högre volatilitetsaversion..
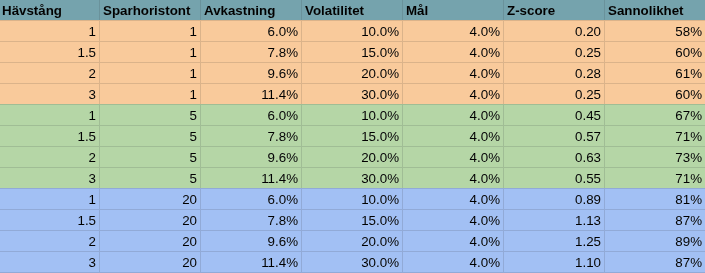
Och tillslut varianten med z-score och sannolikhet att lyckas över viss tidsperiod:
Vi ser igen att hävstången höjer sannolikheten att lyckas jämfört med ingen hävstång!
Slutsats:
- Problemet med sharpe är att den inte tar ens mål i beaktande – man inte kan äta sharpe!
- Vilket är varför vi använder hävstång
- Vanligtvis säger man att riskjusterad avkastning sjunker med hävstång
- Men att öka sin riskjusterade avkastning med hävstång är möjligt, om vi definierar risken som sannolikheten att misslyckas uppnå vårat finansiella mål!
- Likt att investera i riskabla aktier ändå minskar risken att underprestera inflationen jämfört med att lägga pengarna under sängen
- Kom också att tänka på denna tråden: Amortera inte på bostaden---det höjer din risk!
Det finns såkert ännu bättre formler, men jag kände iaf att det var värdefullt att på något sätt få in ens målavkastning i uträkningarna.