Relaterad tråd: En statistisk "gåta" för Taleb-entusiasten
Har inte tänkt så djupt kring ombalansering tidigare, men läste nu ett par artiklar
som fick mig att börja förstå matematiken bakom det (tror jag iaf..)
Artiklarna:
- Unexpected Returns: Shannon’s Demon & The Rebalancing Bonus
- Avoiding The Volatility Trap
- The Iron Law of Volatility Drag
- Maximizing the Rebalancing Premium: Why Risk Parity portfolios are much greater than the sum of their parts
- The Long Term Behaviour of Leveraged ETFs
- Simulating Historical Performance of Leveraged ETFs
- Backtesting Portfolios of Leveraged ETFs
- The Rebalancing Bonus: Theory and Practice
Ombalanseringens “magi” ligger i att volatiliteten minskar,
vilket minskar urholkningseffekten, vilket ökar geometriska snittavkastningen.
Urholkningen sker på grund av att: (1 + x) * (1 - x) = 1 - x^2
Exempel:
En aktie startar på 100 kr och går upp 10%: 100 kr * 1.1 = 110 kr
Nästa dag går aktien ned 10%: 110 kr * 0.9 = 99 kr
Eller: 1 - 0.1^2 = 0.99
Säg att vi nu lägger till 4x hävstång:
Aktien startar igen på 100 kr och går nu upp 40%: 100 kr * 1.4 = 140 kr
Nästa dag går aktien ned 40%: 140 kr * 0.6 = 84 kr
Eller: 1 - 0.4^2 = 0.84
Hävstången är 4x, men urholkningseffekten blev 16x värre, eftersom: 4^2 = 16.
Urholkningseffekten blir alltså exponentiellt värre med ökad volatilitet.
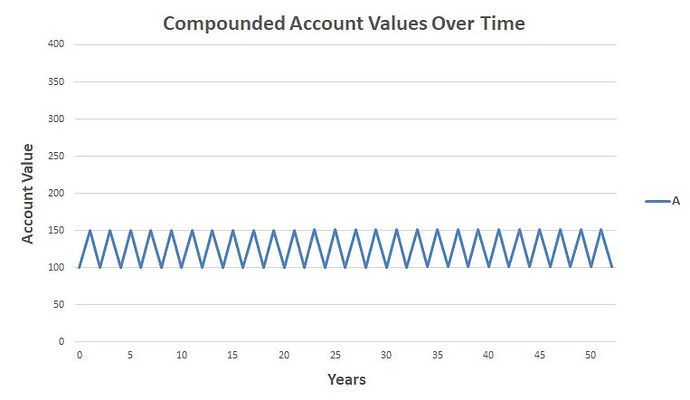
Låt oss tänka oss en aktie som går upp +50% vartannat år och ned -33.3% vartannat år.
Aritmetiska snittavkastningen: (0.5 - 0.333) / 2 = 8.4%
Men geometriska snittavkastningen blir: (1.5 * 0.667)^(1/2) - 1 = 0%
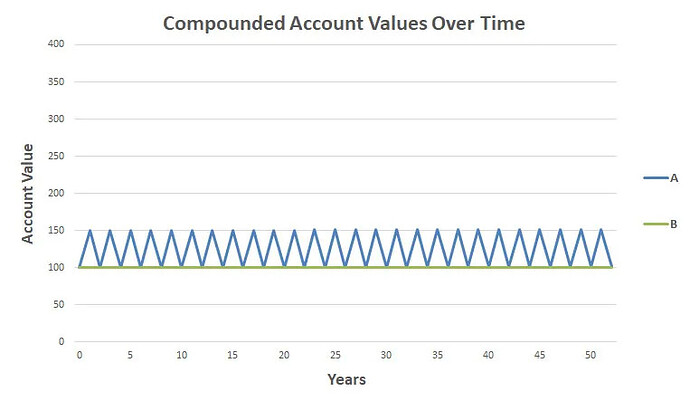
Låt oss nu tänka oss att vi lägger 50% av portföljen i cash istället (0% avkastning och 0% volatilitet), utan att ombalansera.
Våran geometriska avkastning är fortfarande 0%, eftersom det inte uppstår någon synergi
mellan tillgångarna i isolation.
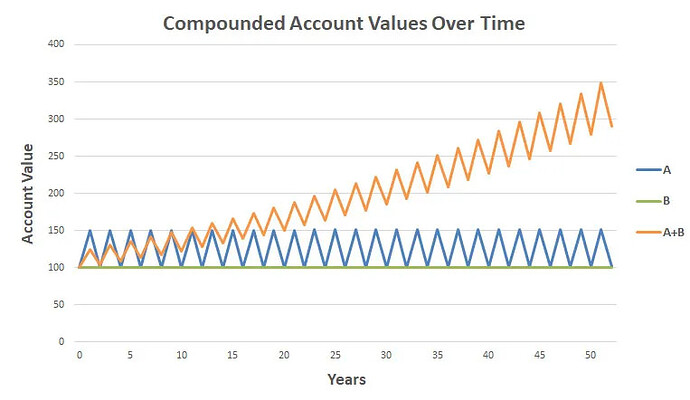
Men när vi varje år ombalanserar dessa två tillgångar så sker det “magiska” –
våran geometriska avkastning ökar till ~2%!
Enligt en av artiklarna ovan så kan man räkna ut en ungefärlig geometrisk snittavkastning
baserat på aritmetiska snittavkastningen och volatiliteten:
Geometriska snittavkastningen är ungefär = Aritmetiska snittavkastningen - (Volatiliteten^2 / 2)
När vi ombalanserar med cash varje år så halveras både aritmetiska snittavkastningen (till 4.2%) och volatiliteten (till 21%), vilket minskar urholkningseffekten, vilket ökar våran geometriska snittavkastning.
Urholkningseffekten minskar alltså mer än aritmetiska snittavkastningen eftersom
volatiliteten upphöjs med två: 0.042 - (0.21^2 / 2) = ~2%
Vi kan också bekräfta detta genom att testa det:
Utan ombalansering
| Period | Aktier, startsumma | Aktier, utveckling | Aktier, Slutsumma | Cash | Total slutsumma |
|---|---|---|---|---|---|
| År 1 | 500 kr | +50% | 750 kr | 500 kr | 1250 kr |
| År 2 | 750 kr | -33,3% | 500 kr | 500 kr | 1000 kr |
| År 3 | 500 kr | +50% | 750 kr | 500 kr | 1250 kr |
| År 4 | 750 kr | -33,3% | 500 kr | 500 kr | 1000 kr |
| År 5 | 500 kr | +50% | 750 kr | 500 kr | 1250 kr |
| År 6 | 750 kr | -33,3% | 500 kr | 500 kr | 1000 kr |
Med ombalansering:
| Period | Aktier, startsumma | Aktier, utveckling | Aktier, Slutsumma | Cash | Total slutsumma |
|---|---|---|---|---|---|
| År 1 | 500 kr | +50% | 750 kr | 500 kr | 1250 kr |
| År 2 | 625 kr | -33,3% | 416,7 kr | 625 kr | 1041,7 kr |
| År 3 | 520,9 kr | +50% | 781,4 kr | 520,9 kr | 1302,3 kr |
| År 4 | 651,2 kr | -33,3% | 434,2 kr | 651,2 kr | 1085,4 kr |
| År 5 | 542,7 kr | +50% | 814,1 kr | 542,7 kr | 1356,8 kr |
| År 6 | 678,4 kr | -33,3% | 452,3 kr | 678,4 kr | 1130,7 kr |
CAGR: (1130,7 kr / 1000 kr)^(1/6) - 1 = ~2%
Som @emilv visade i Taleb-tråden så spelar ordningen på utfallen ingen roll.
(Skillnaden på örena är på grund av avrundningen…)
Med ombalansering, i annan ordning:
| Period | Aktier, startsumma | Aktier, utveckling | Aktier, Slutsumma | Cash | Total slutsumma |
|---|---|---|---|---|---|
| År 1 | 500 kr | -33,3% | 333,4 kr | 500 kr | 833,4 kr |
| År 2 | 416,7 kr | -33,3% | 277,8 kr | 416,7 kr | 694,5 kr |
| År 3 | 347,3 kr | -33,3% | 231,5 kr | 347,3 kr | 578,8 kr |
| År 4 | 289,4 kr | +50% | 434,1 kr | 289,4 kr | 723,5 kr |
| År 5 | 361,8 kr | +50% | 542,7 kr | 361,8 kr | 904,5 kr |
| År 6 | 452,3 kr | +50% | 678,5 kr | 452,3 kr | 1130,8 kr |
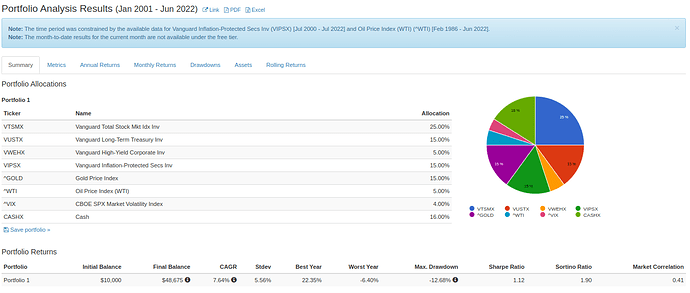
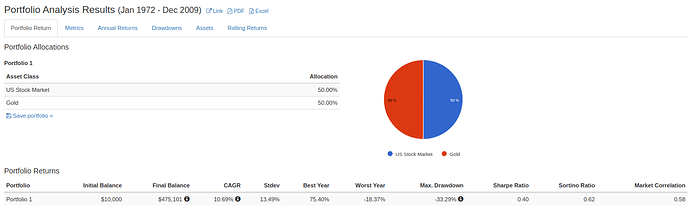
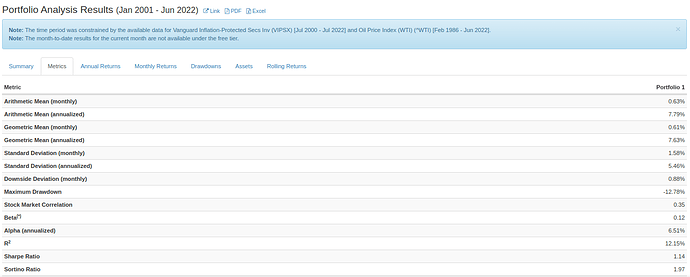
Om vi vill ta ett praktiskt exempel så kan vi kolla på @Zino’s avancerade allvädersportfölj, ombalanserad en gång i månaden (i verkligheten kan andra frekvenser på ombalanseringen vara mer optimal).
Portföljen som helhet
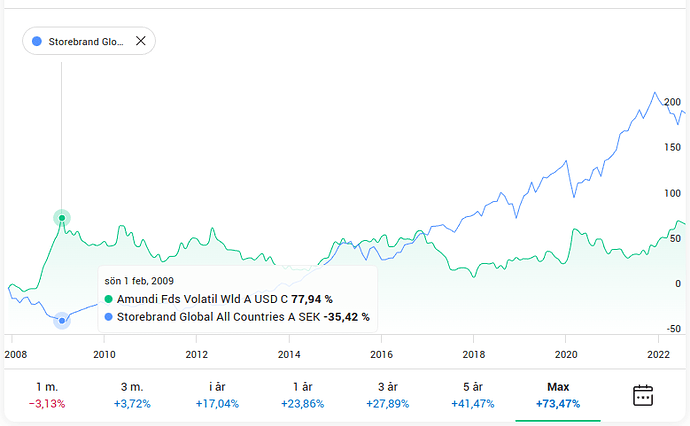
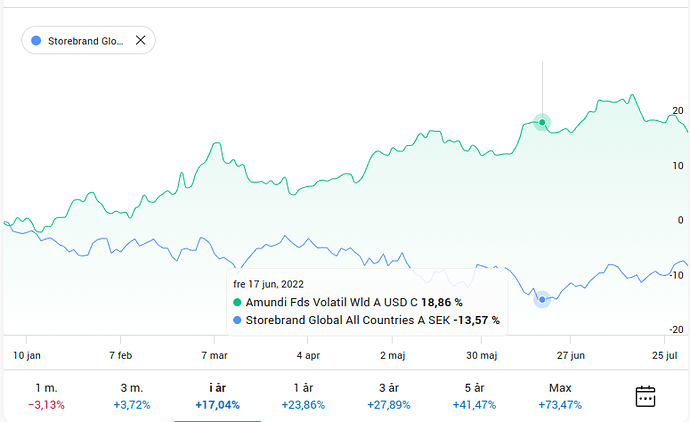
Tillgångarna i isolation
Geometrisk snittavkastning (CAGR) för tillgångarna i isolation:
- 25% Vanguard Total Stock Mkt Idx Inv (VTSMX): 7,27%
- 15% Vanguard Long-Term Treasury Inv (VUSTX): 5,12%
- 5% Vanguard High-Yield Corporate Inv (VWEHX): 5,46%
- 15% Vanguard Inflation-Protected Secs Inv (VIPSX): 4,63%
- 15% Gold Price Index (^GOLD): 9,19%
- 5% Oil Price Index (^WTI): 6,70%
- 4% CBOE SPX Market Volatility Index (^VIX): 0,31%
- 16% Cash (CASHX): 1,31%
Viktat snitt: (7,27%*0,25 + 5,12%*0,15 + 5,46%*0,05 + 4,63%*0,15 + 9,19%*0,15 + 6,70%*0,05 + 0,31%*0,04 + 1,31%*0,16) = 5,49%
Allvädersportföljens faktiska CAGR: 7,64%
Ombalanseringseffekt: 7,64% - 5,49% = +2,15%-enheter
Utöver den matematiska ombalanseringsbonusen så tänker jag att ombalansering även eventuellt kan dra nytta av marknadens ineffektivitet genom momentum och värdefaktorerna – alltså “köpa lågt (värdefaktorn) och sälja högt (momentumfaktorn)”.
“Helheten är mer än summan av delarna” ![]()