Liten uppdatering av portföljen: Optimal strategi för insättningar/månadssparande!
Månadssparande har diskuterats flitigt i den här tråden under den senaste månaden. Tidigare rekommenderade jag helt enkelt att varje månad köpa det tillgångsslag som var mest underviktat, men jag har insett att frågan är mycket mer komplex. Nu känner jag äntligen att jag har funnit en mer optimal metod!
Bakgrund
Problemet med månadssparande är att varje insättning blir en ombalansering, om man inte köper enligt ursprungsfördelning. I multi-asset-portföljer kallas detta cash flow rebalancing och förespråkas ibland för skatteeffektivitet (ingen försäljning), men på ISK är det mindre relevant. Dessutom avviker man då från den optimala ombalanseringsstrategin – att endast ombalansera när tillgångar går utanför sitt spann.
Flera studier – bl.a. av Vanguard och Daryanani (som båda diskuterats tidigare i tråden) – visar att månadsvis ombalansering sannolikt är för frekvent. Du köper konsekvent ”fallande knivar” och säljer stigande trender för tidigt.
Tidigare diskuterade metoder för månadssparande:
-
Köp sämst presterande tillgångsslag varje månad. Enkel men suboptimal: man “ombalanserar” för ofta och köper fallande tillgångsslag med negativt momentum. Kortsiktigt alltid negativ förväntad avkastning på ens senaste insättning.
-
Köp enligt aktuell fördelning varje månad. Teoretiskt perfekt eftersom alla tillgångsslag behåller sin aktuella fördelning och ombalanseringsstrategin därmed inte rubbas, men opraktiskt då det kräver beräkningar och opraktiskt för ETF:er (ingen fraktionell handel). Ett lite enklare alternativ är att köpa enligt målfördelning istället.
-
Månadsspara i alternativa fonder tills ETF-belopp nås. Teoretiskt bra, men ökar komplexitet pga signifikant ökat antal fonder att bevaka och handla.
Förslag på alternativa courtagefria fonder för tillfälligt månadssparande, avancerade portföljen
- Handelsbanken Global Momentum
- Storebrand Global Value
- Captor Iris
- Captor Aster Global Credit
- Danske Globala Realräntor
- Centaur Commodity
- GULD AVA/TRACKER GULD NORDNET
- Lynx Dynamic
- Spara i korträntefond tills ombalansering triggas. Sparar courtage (eftersom man slipper sälja av för att frigöra kapital för köp) men kostar i utebliven avkastning. Ombalansering triggas i snitt 4 ggr/år för avancerade portföljen, och 1-2 ggr/år för grundportföljen. Kostnaden att stå utanför allvädersportföljen i ett kvartal är ~1,35%. Jämfört med courtagebesparingen på 0,5% blir det därmed mindre fördelaktigt.
Uträkning av siffror i metod 4
Årlig överavkastning (över riskfri ränta) för allvädersportföljen uppskattas ligga kring 5,5%. Ett år har i snitt 251 börsdagar.
- Förväntad daglig avkastning: (1 + 5,5%)^(1/251) - 1 = 0,02133% per dygn.
- Kostnad att stå utanför marknaden per:
- vecka: (1 + 0,02133%)^5 - 1 = 0,1067%
- månad: (1 + 0,02133%)^21 - 1 = 0,4489%
- kvartal: (1 + 0,02133%)^63 - 1)= 1,3527%
Avancerade portföljen innehåller 10 olika unika tillgångsklasser. Ombalansering triggas i snitt var 3:e år. Detta innebär i snitt 1 ombalansering var 0,3:e år, dvs var 3,6:e månad. På 1 år blir det alltså i snitt 4 ombalanseringar.
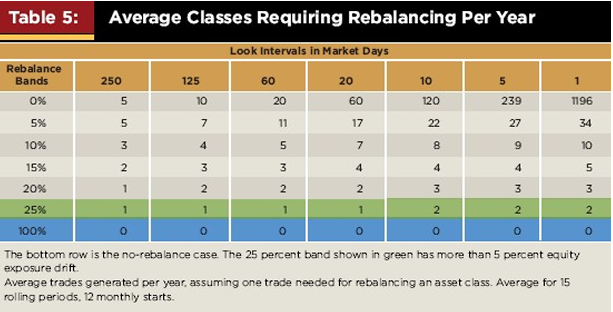
Detta stämmer också med siffrorna från Daryananis artikel:
Genomsnittligt antal ombalanseringar per år för en portfölj med 5 unika tillgångsslag. Vi ser att för ombalanseringsspann 15% och daglig utvärdering av portföljen triggas ombalansering i snitt 5 ggr/år.
Ny metod: köp både sämst och bäst
Efter mycket research och reflektion har jag landat i en kompromiss: varje månad köper vi både det tillgångsslag som gått sämst (mean reversion) och det som gått bäst (momentum)!
Att bara köpa det tillgångsslag som gått bäst (relativt momentum) är en vedertagen strategi som studerats extensivt. Meb Faber (upphovsmannen bakom GTAA) publicerade 2010 artikeln “Relative Strength Strategies for Investing”, där man utgår från ett universum med aktier (USA), aktier (globala), långa statsobligationer, råvaror och REITs. Varje månad köptes enbart de tillgångsslag som presterat bäst:
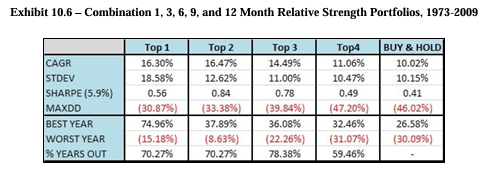
I denna tabell sammanställs avkastningen för strategin för olika portföljer som väljer top 1-3 av tillgångsslagen, varje månad. För att avgöra bäst presterande tillgångsslag tas ett snitt av 1, 3, 6, 9 och 12-månaders avkastning.
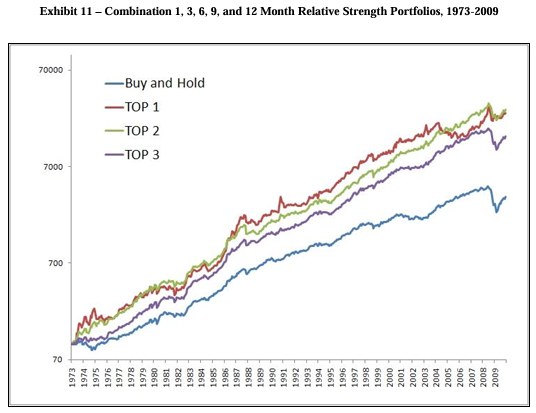
Samma siffror som ovan i graf. Vi ser att relativt momentum klart överpresterar buy-and-hold.
Tabellen från artikeln visar alltså att strategin presterat bäst när man investerat i de 2 bäst presterande tillgångsslagen varje månad. Ska man välja enbart en tidshorisont att titta på för att avgöra bäst presterande tillgångsslag har 6-månaders avkastning presterat bäst.
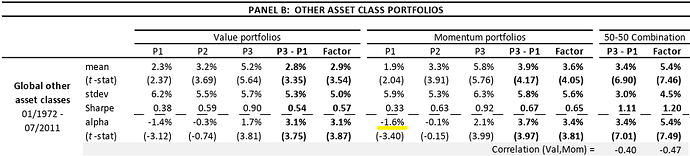
En annan välkänd artikel på ämnet är “Value and Momentum Everywhere” av AQR, som publicerades 2012. I artikeln dras samma slutsats som ovan, samt att en strategi som varje månad köper de tillgångsslag som presterat sämst underpresterar en likaviktad portfölj:
Tabell ur artikeln som visar att en portfölj P1 som varje månad väljer den tredjedel tillgångsslag med sämst momentum underpresterar en likaviktad portfölj med 1,6%-enheter, medan en portfölj P3 med bäst momentum överpresterar med 2,1%-enheter.
Varför då inte enbart månadsspara i det bäst presterande tillgångsslaget, och bara köpa underviktade när ombalansering triggas? Det är ingen dålig strategi, men problemet är:
- Portföljen blir mer obalanserad, och volatiliteten kan därmed förväntas öka.
- Portföljen blir mer känslig för momentum krasches (se denna artikel från 2013 av Moskowitz för beskrivning av detta fenomen), som uppstår i tider då börsen snabbt skiftar efter en utdragen trend.
- Ökade transaktionskostnader, eftersom vi hela tiden påskyndar ombalansering av det överviktade.
Genom att köpa både det tillgångsslag som gått sämst respektive bäst får vi alltså det bästa av två världar:
- Bibehåller balans i portföljen, vilket minskar volatilitet och ökar ombalanseringspremien. Kan ses som den enklaste proxyn till att månadsspara i hela portföljen.
- Neutralt i momentum, eftersom tillgångsslagen tar ut varandra. Kvar blir tillgångsslagens riskpremie i förväntad avkastning.
- Minskad känslighet för momentumkrasch genom att ta lika stor position i mean reversion.
- Oförändrade transaktionskostnader, eftersom vi minskar antalet ombalanseringstriggers hos underviktat samtidigt som vi påskyndar ombalansering av överviktat.
- Psykologiskt lättare att 50% av ens senaste insättning oftast stiger, jämfört med att 100% oftast sjunker.
- Relativt simpel metod som inte kräver några tidskrävande kalkyler att utföra.
Optimalt köpbelopp för ETF:er
Fram tills nu har jag rekommenderat att eftersträva köp på minst 3600 kr för ETF:er, eftersom det är detta köpbelopp som krävs för att erhålla lägsta courtage på 0,25% på Nordnet. Jag har dock insett att optimalt köpbelopp bättre baseras på förväntad kostnad av att stå utanför marknaden. Följande insikt gjorde mig ganska exalterad (ping @bspastikern som väckte tanken i detta inlägg).
Min tidigare uträkning i detta avsnitt var helt felaktig, tack @Mellan för påpekande. Här följer en korrigerad uträkning:
Vi börjar med att räkna ut var brytpunkten går för när det lönar sig bättre att månadsspara varannan månad (tillfälligt sparande i korträntefond), kontra varje månad:
Antaganden:
- Förvåntad månadsavkastning över riskfri ränta (se ovan under “bakgrund”): 0,4489%
- Minsta courtage Nordnet: 0,25% eller 9 kr (köp <3600 kr innebär alltså courtage >0,25%)
Förväntad avkastning vid köp varje månad:
(x - 9) * 1,004489 + (x - 9)
Där (x - 9) är köpesumman efter avdrag för courtage.Förväntad avkastning vid köp varannan månad:
2x - 2x/400
Där 2x/400 är courtaget på 0,25%. Jag räknar med detta istället för 9 kr då efterföljande uträkning visar att summan blir >3600 kr. Notera även att vi inte behöver beräkna någon ränta på dessa pengar då det är avkastning över riskfri ränta som avses i alla beräkningar.När är dessa summor lika?
(x - 9) * 1,004489 + (x - 9) = 2x - 2x/400
x = 1901 kr
Månadsspar under 1901 kr lönar sig alltså bättre att lägga tillfälligt i en korträntefond och köpa ETF:er varannan månad istället. Men när börjar löna det sig med var tredje månad?
För att räkna ut detta behöver vi beräkna förväntad avkastning till minsta gemensamma nämnare för 2 och 3, dvs månad 2 * 3 = 6.
Förväntad avkastning vid köp varannan månad:
1,004489^4 * (2x - 9) + 1,004489^2 * (2x - 9) + (2x - 9)
Där (2x - 9) är köpet efter avdrag för courtage. Första köpet hinner alltså växa under 6 - 2 = 4 månader, andra under 2 månader, och sista inte alls.Förväntad avkastning vid köp var tredje månad:
1,004489^3 * (3x - 9) + (3x - 9)
Första köpet hinner alltså växa under 6 - 3 = 3 månader, andra inte alls.När är dessa summor lika?
1,004489^4 * (2x - 9) + 1,004489^2 * (2x - 9) + (2x - 9) = 1,004489^3 * (3x - 9) + (3x - 9)
x = 672 kr
Vi ser att både vänster led och höger led blir geometriska summor, med fler och fler termer ju lägre frekvensen blir för månadsköp. Vi kan därmed skriva detta som en generell formel:
Minsta gemensamma nämnare för n och (n + 1) = n(n + 1) månader.
Förväntad avkastning vid köp var n:te månad:
1,004489^(n * n) * (nx - 9) + 1,004489^(n(n - 1)) * (nx - 9) + … + 1,004489^0 * (nx - 9)
Första köpet hinner alltså växa under n(n + 1) - n = n * n månader, andra under n(n-1) månader, osv.Detta kan skrivas som en geometrisk summa: (nx - 9) * (1,004489^(n(n + 1)) - 1)/(1,004489^n - 1)
Förväntad avkastning vid köp var (n + 1):te månad:
1,004489^((n + 1)(n - 1)) * (x(n + 1) - 9) + 1,004489^((n + 1)(n - 2)) * (x(n + 1) - 9) + … + 1,004489^0 * (x(n + 1) - 9)
Första köpet hinner alltså växa under n(n + 1) - (n + 1) = (n + 1)(n - 1) månader, andra under (n + 1)(n - 2) månader, osv.Detta kan skrivas som en geometrisk summa: (x(n + 1) - 9) * (1,004489^((n + 1)n) - 1)/(1,004489^(n + 1) - 1)
När är dessa summor lika?
(nx - 9) * (1,004489^(n(n + 1)) - 1)/(1,004489^n - 1) = (x(n + 1) - 9) * (1,004489^((n + 1)n) - 1)/(1,004489^(n + 1) - 1)
Vi kan bryta ut x ur ovanstående ekvation, och beräkna för olika värden på n:
| Månadsspar Nordnet (Mini) | Månadsspar Avanza (Mini) | Minsta ETF-köp Montrose (Access) | Rek. ETF-köpfrekvens |
|---|---|---|---|
| >1901 kr | >211 EUR | >4252 kr | Varje månad |
| 672 - 1901 kr | 75 - 211 EUR | 1419 - 4252 kr | Var 2:a månad |
| 337 - 672 kr | 37 - 75 EUR | 711 - 1419 kr | Var 3:e månad |
| 202 - 337 kr | 22 - 37 EUR | 427 - 711 kr | Var 4:e månad |
| 135 - 202 kr | 15 - 22 EUR | 285 - 427 kr | Var 5:e månad |
Antaganden:
- Minsta courtage Nordnet (Mini): 0,25% eller 9 kr (köp <3600 kr innebär alltså courtage >0,25%)
- Minsta courtage Avanza (Mini): 0,25% eller 1 EUR (köp <400 EUR innebär alltså courtage >0,25%)
- Minsta courtage Montrose (Access): 0,15% eller 19 kr (köp <12667 kr innebär alltså courtage >0,15%)
Observera att syftet med ovanstående tabell bara är att ge en fingervisning. I realiteten är månadsavkastningen förstås inte konstant, utan varierande, och de absoluta skillnaderna i slutsummorna är relativt små även om man råkar köpa ETF:er för lägre summor än rekommenderat. I praktiken rekommenderas inte att ligga utanför marknaden >3 månader, utan man bör då överväga alternativa metoder.
Baserat på storlek på månadssparande kan det alltså lämpa sig matematiskt bättre att köpa en korträntefond och invänta köp än att köpa ETF:en direkt. Vi ser att Montrose generellt lämpar sig dåligt för små köpesummor. Ett alternativ till ovanstående (för att slippa ligga utanför marknaden) är att köpa tillfälliga alternativa courtagefria fonder såsom beskrivet i metod 3 ovan.
Sammanfattning:
Jag har insett att insättningar och månadssparande i allvädersportföljen kompliceras av flera faktorer, däribland att man vill undvika att köpa tillgångar med negativt momentum och att ETF:er inte bör handlas i för små poster pga ökat courtage. Jag har nu definierat en optimal metod för insättningar och månadssparande i allvädersportföljen:
-
Vid stora insättningar som räcker till att köpa alla tillgångsslag: köp allt enligt aktuell fördelning (1:a hand) eller målfördelning (2:a hand) i möjligaste mån. Blir aldrig helt exakt eftersom ETF:er måste handlas i hela andelar.
-
Vid mindre insättningar/månadsspar: köp 50% i den fond som är mest underviktad, och 50% i de 1-2 fonder som gått bäst under senaste 1-12 månaderna alt. 6 månaderna (sistnämnda enklare men lite mindre robust).
- Om detta är för krångligt, välj de 1-2 mest överviktade fonderna i portföljen som proxy för 1-12 månaders avkastning.
- Om detta skulle knuffa en stigande fond över sitt ombalanseringsspann, hoppa över den alt. dela upp insättningen över fler fonder.
-
Eftersträva ETF-köp på minst 1901 kr vid månadssparande. Detta är den gräns då förväntad månadsavkastning i allvädersportföljen överstiger den ökade courtagekostnaden över lägsta courtage.
- Vid månadssparande <1901 kr, överväg att spara i tillfälliga alternativa courtagefria fonder, alternativt spara i korträntefond tills brytpunkt uppnås (se tabell ovan i detta inlägg).
Siffran 1901 kr gäller Nordnet. För Avanza är motsvarande siffra 211 EUR och för Montrose 4252 kr.
Tycker man att allt ovanstående verkar för komplext går det utmärkt att månadsspara på vilket sätt man vill, portföljen faller inte på det. Denna uppdatering kommer endast göra skillnad på marginalen, men det känns samtidigt väldigt skönt att äntligen ha definierat en optimal metod för något så basalt som månadssparande.
Vad tror ni om ovanstående metod, känns den praktiskt genomförbar? Jag kommer att uppdatera första inlägget del 3a samt tidslinjen med ovanstående. Stort tack för ert intresse, jakten på den “ultimata” allvädersportföljen fortsätter!