Jakten på den "ultimata" allvädersportföljen

Spara och investera Portföljer och allokering
,
3706

Tack för förtydligandet! Jag uppfattar det som att vi i grunden är överens om att marknadsportföljen är en teoretiskt motiverad baseline i ett CAPM/ICAPM-liknande modeller, medan mycket av argumentationen för allväders/ riskparitetsportföljer i praktiken bygger på empiri och historiska korrelationer.

Det är iaf ungefär där jag själv landar. Jag ifrågasätter inte att riskparitet kan fungera rent praktiskt, eller att lägre drawdowns och jämnare utveckling är attraktiva egenskaper. Min fundering gäller snarare i vilken mening de kan kallas ”ultimata” om det saknas en sammanhållen modell som säger att konstruktionen utgör ett teoretiskt optimum relativt ett enkelt marknadsviktat aktie och räntebenchmark.

Ska bli intressant att läsa när du utvecklat din definition av ”ultimat” och hur du tänker kring den teoretiska modellen bakom.

1 gillning
3707

Ja, vi är i grunden överens om mer än vad vi inte är, skulle jag säga. Dock håller jag absolut inte med om det fetmarkerade.

Precis som CAPM antar att marknaden “ser” volatilitet och korrelationer med den optimala marknadsportföljens beta (för att avgöra prissättning av tillgångar eftersom beta är den enda relevanta faktorn), antar riskparitet att marknaden “ser” volatilitet och korrelationer hos enskilda tillgångsslag som utgör den optimala allvädersportföljen. Antagandet om en effektiv marknad är exakt detsamma, vilket artikeln jag länkade beskriver utförligt, och som jag kommer förklara bättre i mitt kommande inlägg. Den enda skillnaden är som sagt vad man tror att marknaden belönar - enbart beta eller oberoende riskpremier?

3 gillningar
3708

Håller med om att både CAPM och riskparitet kan beskrivas som ramverk där marknaden ”ser” risk i form av volatilitet och korrelationer.

Min invändning gäller snarare vad som faktiskt kan härledas som ett jämviktsresultat. I CAPM/ICAPM finns ett etablerat teoretiskt argument som leder till marknadsportföljen som ett optimum under relativt tydliga antaganden. Modeller som FF3/FF5 förnekar inte flera riskkällor, men de säger inte att man genom konstruktion kan få bättre riskjusterad avkastning än marknadsportföljen i en effektiv marknad.

Riskparitet är i grunden en riskallokeringsregel, inte en avkastningsmodell. Den kräver inte ens att de ingående tillgångarna har positiv förväntad avkastning, bara att de har volatilitet och korrelationer. Att riskparitetsportföljer historiskt fungerat väl beror därför på empiriska omständigheter och val av tillgångar, snarare än på ett generellt jämviktsargument.

Det är i den bemärkelsen jag tycker att formuleringar om att synsättet är ”mer verklighetsförankrat” blir starka. De beskriver empiri väl, men går längre än vad teorin i sig kan bära.

Komplettering:
När jag tänker lite noggrannare på vad som faktiskt måste antas för att en AW/RP-portföljer ska kunna få högre riskjusterad avkastning än marknadsportföljen, landar jag i följande antaganden:

  • Att volatilitet är det relevanta riskmåttet.

  • Att historiska korrelationer är tillräckligt stabila över tid.

  • Att riskpremier existerar även för risker som i princip går att diversifiera bort.

  • Att marknaden inte redan har prisat dessa risker optimalt.

  • Att rebalansering i sig ger positiv förväntad avkastning efter avgifter.

Inget av dessa antaganden är orimligt var för sig. Däremot följer inget av dem av etablerade jämviktsmodeller. I en effektiv marknad där marknadsportföljen är mean variance effektiv finns det inget som säger att dessa antaganden måste hålla samtidigt.

1 gillning
3709

Hej. Den svåraste komponenten för mig att få till i en svensk allvädersportfölj är statsobligationerna. Det känns som att antingen sitter man med massa valutarisk om man använder ETF:er med utländska statspapper med lång duration (20+ år) eller så blir durationen för kort med de svenska räntefonder som finns. Det fick mig att titta på möjligheten att själv köpa svenska statsobligationer på andrahandsmarknaden (samt nya när man behöver rulla befintliga). Och det finns ett par obligationer som har lång duration (utöver standard-10-åringarna), t ex:

  • SGB 1064 (maturity 2071)

  • SGB 1063 (maturity 2045)

  • SGB 1053 (maturity 2039)

Om långräntedelen i ens portfölj är så pass stor att man kan köpa dessa på egen hand, hur ser ni på att bygga kring dessa?

1 gillning
3710

Tänka utanför boxen, men lite väl komplicerat möjligen. Överväger hellre att helt byta ut räntorna mot stil. Egentligen hittills bara realräntorna som sänker portföljen. Misstänker att ett rakt byte mot stil hade gett ±0, kanske bl.a. lägre avkastning och högre drawdown då man eventuellt får lägre SEK-hedge . Så håller nog fast vid räntedelen tills vidare.

3711

Intressant tanke! Var har du hittat dessa obligationer tillgängliga för köp, och hur mycket kostar en andel? Det vore absolut möjligt, men jag tror tyvärr att det blir både krångligare och sämre än att bara köra på Captor Iris.

Captor Iris har ändå en imponerande duration på 11,2 år i skrivande stund, för att vara en “vanlig” svensk räntefond. Dessutom är förväntad avkastning på de säkerställda bostadsobligationerna i Captor signifikant högre än svenska statsobligationer, trots identiskt kreditbetyg AAA. I skrivande stund ligger förväntad avkastning hos Captor Iris på 4,02%, medan en svensk 10-åring ligger på 2,79%.

Jag är glad över att vi har tillgång till Captor I vårt svenska fondutbud, vi har haft en norrman här i tråden tidigare som beklagat sig över att de endast har tillgång till mellanmjölksräntefonder med max 5 års duration. Då hade jag varit mycket mer intresserad av att köpa obligationer direkt.

1 gillning
3712

Tack Zino.

Alla utstående statspapper hittar du här:

För att handla på andrahandsmarknaden så är det storbankerna som gäller. Minsta post 1 msek.

När det gäller långräntedelen så är jag lite old school och vill ha instrument som skyddar vid ekonomisk kollaps och finansiell panik. Kreditbetyg ger jag inte mycket för. Har kanske sett The Big Short för många gånger.

Dessutom är ju 11,2 år väldigt kort duration jämfört med 25-30 år som Harry Browne förespråkar.

2 gillningar
3713

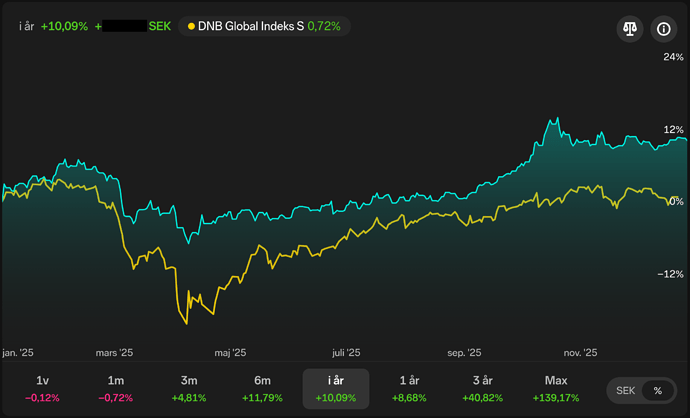
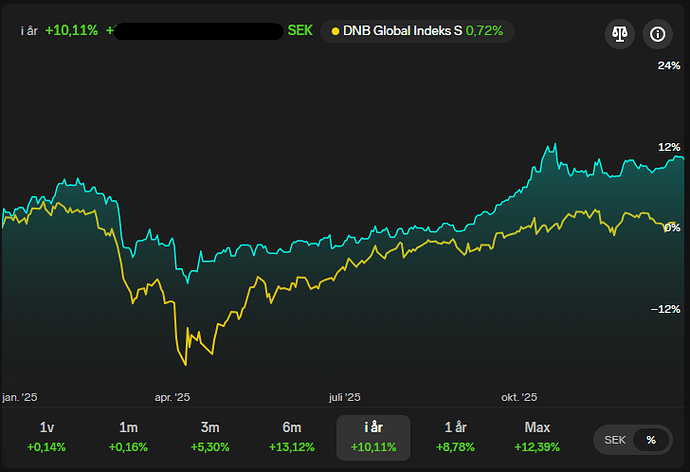
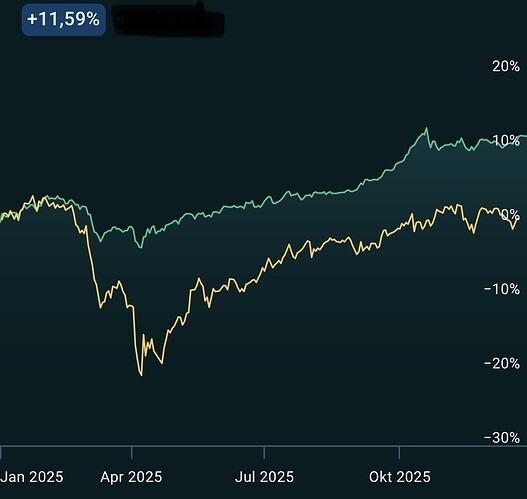
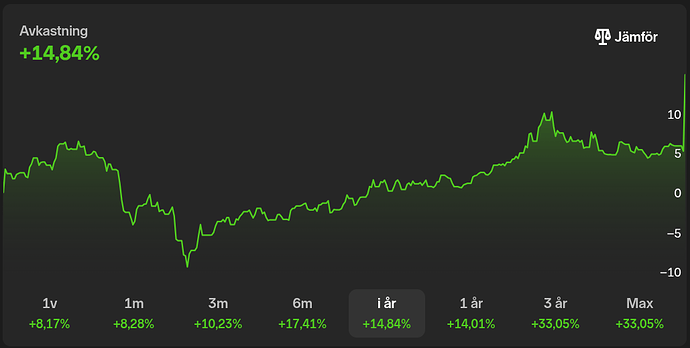
Starkt inspirerad av ovan artikel, samt denna uppföljande artikel, så har jag lagt till de flesta av modellerna som diskuteras till Ex-Ante Playground, och dessutom en praktisk implementation av Markovitz (long-only mean-variance) och en kombination av Equal Risk Contribution + Markovitz.

Man kan alltså välja att optimera viktningen av en portfölj (eller alla) enligt någon av dessa modeller och se vad utslaget blir för förväntad avkastning, sharpekvot mm. Vill man jämföra samma portfölj med olika viktningar så gör man först en kopia av portföljen och applicerar viktningen på kopian.

Koppling till den ultimata allvädersportföljen lämnar jag för diskussion :slight_smile:

Viktning

Viktning av portföljens innehav görs antingen manuellt, eller beräknas enligt olika modeller som är mer eller mindre naiva, beroende på tillgänglig information och/eller personlig åsikt om vilken information som är pålitlig. Modellerna listas nedan i fallande naivitetsgrad.

Likaviktad

Varje innehav får samma vikt oavsett risk, förväntad avkastning och korrelationer.

Marknadsviktad

Varje innehav är viktad enligt nuvarande marknadsvikt. Obs, behöver ställas in manuellt.

Inverse Variance

Parametrar: volatiliteter (σ)
När innehaven har liknande förväntad avkastning, och då korrelationerna är okända (eller homogena) så är den optimala portföljen viktad enligt inversen av innehavens varians (σ^2).

Inverse Volatility

Parametrar: volatiliteter (σ)
När innehaven har liknande förväntad Sharpekvot, och då korrelationerna är okända (eller homogena) så är den optimala portföljen viktad enligt inversen av innehavens volatilitet.

Maximum Decorrelation

Parametrar: korrelationer (ρ)
När innehaven har liknande förväntad Sharpekvot men varierande korrelationer så är den optimala portföljen viktad så att mängden dekorrelation mellan innehaven är maximerad.

Minimum Variance

Parametrar: volatiliteter (σ) och korrelationer (ρ)
Liknande Inverse Variance men tar även hänsyn till korrelationer. Effektiv när innehaven har liknande förväntad avkastning. Den försöker minimera påverkan av de innehav som har störst varians (σ^2).

Maximum Diversification

Parametrar: volatiliteter (σ) och korrelationer (ρ)
Baserad på antagandet att marknader är risk-effektiva, dvs att ett mer riskfyllt (volatilt) innehav innebär högre avkastning, så maximerar denna algoritm Diversification Ratio (DR, se egen definition).

Equal Risk Contribution (ERC)

Parametrar: volatiliteter (σ) och korrelationer (ρ)
Viktar portföljen så att varje innehav bidrar med lika mycket risk/volatilitet till portföljen som helhet.

Markovitz

Parametrar: förväntad avkastning (μ), volatiliteter (σ) och korrelationer (ρ)
Teoretiskt den portfölj som är mean-variance optimal, dvs maximerad Sharpekvot, men är svårberäknad i praktiken för en portfölj med endast långa innehav. Tar ej hänsyn till riskparitet. En fjärde parameter, kallad riskaversion (λ) avgör om låg risk ska premieras före hög avkastning.

ERC-Markovitz

Parametrar: förväntad avkastning (μ), volatiliteter (σ) och korrelationer (ρ)
En kombination där portföljens vikter beräknade enligt ERC får ligga till grund för en Markovitz-optimering. Behåller/skapar riskparitet för portföljen samtidigt som den kan pressa upp både riskjusterad och absolut avkastning.

Disclaimer: jag har tagit hjälp av AI för implementationen, och har försökt verifiera/jämföra med de teoretiska formlerna, så se detta som en första beta-version av funktionen.

6 gillningar
3714

Intressant. Själv lutar jag åt någon slags HRP (hierarkisk riskparitet) justerad för avkastning. Jag börjar med att ta fram en ren HRP, utan justering för avkastning. Vi får se var det landar.

1 gillning
3715

För en konkret portfölj med många delvis överlappande innehav så kan en hierarkisk modell vara nödvändig för att ”hålla algoritmen i schack”. För konceptuella portföljer som i ExAP så behövs det nog inte, gjorde mer skada än nytta när jag provade.

2 gillningar
3716

Finns det någon graf man kan få se på hur allvärdersportföljen gick i år?

5 gillningar
3717

Jag tror inte någon följer exempelportföljen strikt, inte ens @Zino, eftersom den ändras då och då, och det skulle bli dyrt att ständigt hålla på att byta värdepapper till något som är nästan samma – fast kanske lite bättre. Exempelportföljen är mer ett förslag på vad man kan köpa om man startar en portfölj i dag.

Hursomhelst, så här ser mitt utfall ut för i år. Min portfölj har stora likheter med exempelportföljen, eller med hur exempelportföljen sett ut historiskt. I vissa avseenden är den framåtblickande mot hur jag tror att exempelportföljen kan komma se ut framöver. Jag har exempelvis bytt ut delar av stil mot Mandatum Mngd Ftrs A1 SEK Cap Perf H och :united_kingdom: BH Macro Ltd.

Men i stora drag är detta ändå en lätt modifierad variant av exempelportföljen.

image
image2451×1488 322 KB

10 gillningar
3718

Tack snälla :grinning_face::+1: Mvh

1 gillning
3719

Ha, jag slår dig med 0,02% :slight_smile:

image
image728×498 41.5 KB

(smög in ett litet mellandagsskämt också)

5 gillningar
3720

Och som tröst för er/oss som lite väjer för avancerade portföljens komplexitet så gick en helt ”vanlig” Permanentportfölj med 25% kort-/långräntor, globalindex och guld så här:

IMG_4221
IMG_42211170×1108 78.1 KB

Edit: Hade gärna benchmarkat mot grundportföljen under lite icke inprisad inflation och tillväxt för att se vad frånvaron av råvaror har för effekt.

8 gillningar
3721

Över tid så kan råvaror antas ha ganska låg korrelation mot övriga tillgångsslag i grund- eller permanentportföljen, så vilken som förväntas gå bäst handlar i princip bara om du tror att råvaror har någon riskpremie eller ej (sparkonto som bekant saknar ju riskpremie).

2 gillningar
3722

Tack för din kommentar. Uppskattar all feedback.

Jag antar att korta räntorna bidrar både till sänkt total avkastning och samtidigt till minskad volatilitet. Det senare både pga lägre riskpremie och att de via ombalansering kan kapa toppar och dalar för övriga komponenter.

Råvarors låga korrelation mot aktier/långräntor/guld bör väl ge likartad effekt med lägre svängningar men på lång sikt högre avkastning pga högre riskpremie.

Det är väl hela tiden detta man spelar med i allvädersportföljerna. Att laborera med olika delkomponenter för att minska volatilitet och samtidigt hålla uppe avkastningen.

Det sägs att man endast ska investera i sådant man förstår. Jag ser det som att jag då själv bör kunna välja ut en lämplig produkt, även om RT plötsligt skulle försvinna. Jag är tveksam till att jag skulle klara det avseende råvaror. Jag har en sådan liten portfölj också men jämför gärna med en Permanentportfölj. Jag ser PP som en potentiell stay-rich-portfölj (tillräckligt bra @Viss-vädersportfölj”) som jag förstår mig på själv. Dessutom löser den rådet att ha viss summa av framtida behovet (”5 år”) i korta räntor.

Inlägget är tänkt för de, som jag, som kanske i onödan avstår även väldigt förenklad (obalanserad enligt originalinlägget) AW-variant. Även sådana kan bete sig hyggligt bra (åtminstone periodvis) med 1-årsavkastning 11,3%, Sharpe 1,54 och standardavvikelse 6,27%.

Jag är grymt imponerad av nivån på diskussionen kring det optimala alternativet men tycker det är kul ibland att kanske trösta oss andra med att det inte är hopplöst att hålla det enklare.

7 gillningar
3723

Absolut, en permanentportfölj är väldigt mycket bättre än många andra alternativ, så trivs du bra med den så är det bara att köra på.

För att nyansera detta lite. Jag tror mycket att det beror på personlighetstyp, men jag tycker också att det finns grader av förståelse, och att man måste jobba med en sorts förenkling/förädling av tillgänglig information. För egen del så skulle jag aldrig ha kommit igång med en avancerad portfölj om jag kände att jag behövde förstå varje liten detalj på samma nivå som @zino. Däremot så känner jag mig kompenent/trygg nog att bedöma “kvaliteten” på informationen som finns här, nog mycket för att lita på och köra på den.

Det rådet, X antal år, behöver matchas med vad resten av kapitalet är investerat. För X =5 är det gissningsvis en aktietung portfölj med stor drawdown. För en PP/AW-portfölj så är det onödigt mycket kapital som hade kunnat generera avkastning.

7 gillningar
3724

@zino, hur kommer det sig att mer än hälften av din årsavkastning på Shareville uppstått typ i dag?

Är det Nordnet som trollar, eller är det du som har gjort värsta trejden som inte har dykt upp under Aktivitet ännu?

image
image1029×520 36.6 KB

2 gillningar
3725

Jag har sett liknande saker ske om man gör köp eller sälj, och då korrigerar sig grafen under dagen / till dagen efter. Dvs det är ett “fel” i grafen som blir rätt sen.

Kan se i portföljen:

"för 3 tim sedan
Köpte Captor Aster Global Credit A](Captor Aster Global Credit A - Jämför och köp fonder | Nordnet) till 291,97 SEKÖkade position med 11.43 %

23 dec.
Minskat innehavet i [Amundi Physical Gold ETC (C)] till 150,77 EUR
Minskade position med 10.42 %"

Se ju ut att vara en matchande sälj och köp om ca 11% som kanske får grafen att hoppa till.
Kan det vara så @Zino?

1 gillning