Tack till alla inblandade för hjälpen med att reda ut detta, särskilt @CarlJohan, @Slumpvandraren och @Polyfalante. Jag hade själv också missförstått detta.
Kontentan är alltså att Sharpe för en portfölj aldrig kan stiga med hävstång, så länge lånekostnaden >= riskfria räntan.
Övertygande exempel på ovanstående mha Excel
Jag skapade även ett kalkylblad i Excel för att säkerställa att ovanstående stämmer och få bättre förståelse för dynamiken:
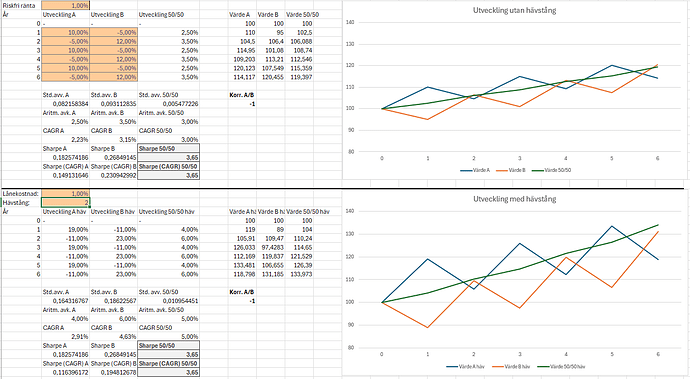
Här ser vi utvecklingen av två portföljer: utan hävstång (ovan) samt med hävstång (nedan). Varje portfölj består av två tillgångar: 50% A (blå linje) och 50% B (orange linje). Portföljens utveckling är den gröna linjen. Ombalansering till målvikt sker i slutet av varje år. Värden i de orangea rutorna har jag fyllt i själv, resten är uträkningar.
Vi ser att med ovanstående korrelation på -1 (mer korrekt 0,99… eftersom -1 ger oändlig Sharpe) mellan A och B har den obelånade portföljen Sharpe 3,65 (både “traditionell” Sharpe samt CAGR-Sharpe). Den belånade portföljen med hävstång 2x har identisk Sharpe, när lånekostnad = riskfri ränta.
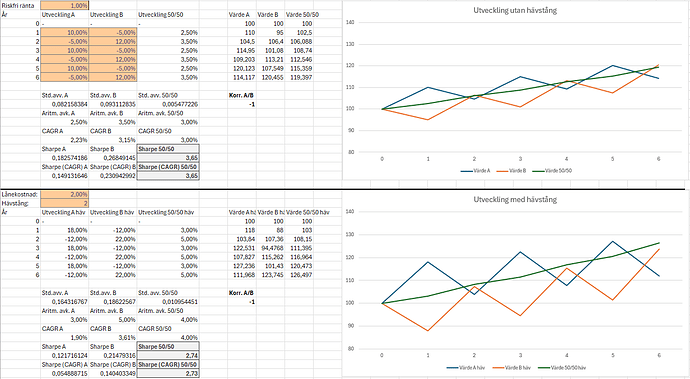
Här har jag höjt lånekostnaden till riskfri ränta + 1%-enhet. Den belånade portföljens Sharpe sjunker då till 2,74.
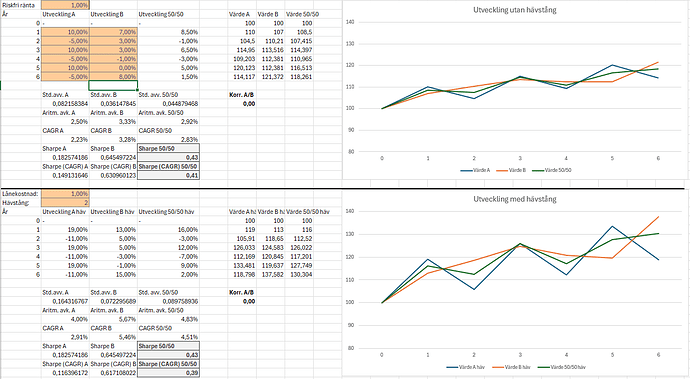
Här har jag ändrat tillgång B så att CAGR är nästan samma som innan, men korrelationen med A är 0 istället för -1. Sharpe sjunker då kraftigt till 0,43, och CAGR-Sharpe ännu mer. Den belånade portföljen har dock fortsatt identisk Sharpe (men inte identisk CAGR-Sharpe) eftersom lånekostnad = riskfri ränta.
Det stämmer. Ombalanseringspremien skulle aldrig adderas, det är bara en del av den geometriska avkastningen.
Bör inte denna formel snarare vara:
RP =\frac{{1}}{{2}}{{(\sum_{{i=1}}^{{n}} w_i (\lambda\sigma_i)^2)}} - \frac{(\lambda\sigma_p)^2}{2}