Volatilitetsförluster (svar)
För att avsluta den här arbetsveckan tänkte jag passa på att skriva några rader om volatilitetsrelaterade förluster och vinster. Frågan har tagits upp av bland annat @Preppern och @RobertK.
Nästa vecka är alla stockholmare på sportlov (jag kommer från Uppsala) så då kommer jag förhoppningsvis kunna svara lite snabbare på frågor från det här forumet än vad jag gjort hittills.
Volatilitetsrelaterade vinster och förluster gäller alla portföljer som justeras för att hålla konstanta vikter. Dessa är inte unika för produkter med hävstång. För att göra resonemanget som följer lite enklare tänker vi oss att den portfölj som ombalanseras för att hålla konstanta vikter bara består av två tillgångar. Tillgångarna kan vara vad som helst, men det mest naturliga valet är att låta de vara aktier och obligationer.
Tänk er en portfölj vars målsättning är att alltid ha andelen w investerat i aktier och den resterade delen, 1-w i obligationer. I en traditionell “60/40”-portfölj är andelen aktier 60 procent (d.v.s. w är 60%) och andelen obligationer är 40 procent (d.v.s. 1-w är 40%). Så fort marknaden rör sig kommer dessa andelar dock att ändras. Den tillgång som har gått bäst kommer att ha fått en högre vikt relativt den andra.
Vi kan exempelvis anta att aktier under någon period går upp med 10% och att utvecklingen för obligationer samtidigt är noll. Vikten för aktier i portföljen är nu 62.3 procent:
(1+10%)×60% / [ (1+10%)×60% + (1+0%)×40% ] = 62.3%
För att åtgärda detta behöver den tillgång som gått bäst säljas och den tillgång som gått sämst köpas. Om aktier har går bättre än obligationer kommer investeringsstrategin att sälja aktier och köpa obligationer. Om å andra sidan aktier har gått sämre än obligationer kommer investeringsstrategin att sälja aktier och köpa obligationer.
Investeringsstrategin kommer alltså hela tiden att sälja det som relativt sett är ”dyrast” och köpa den tillgång som relativt sett är ”billigast”. Att konsekvent handla på detta sätt kommer innbära att en vinst eftersom strategin ”köper billigt och säljer dyrt” och detta ger en ”volatilitetsvinst”.
För investeringsstrategin i Global Plus gäller att andelen aktier är 140 procent (d.v.s. w är 140%) och andelen obligationer är minus 40 procent (d.v.s. 1-w är -40%, aktieexponeringen är belånad). Så fort marknaden rör sig kommer dessa vikter dock att ändras.
Vi kan exempelvis igen anta att aktier under perioden gått upp med 10 procent och att utvecklingen för obligationer är noll. Vikten för aktier i portföljen är nu 135.1 procent:
(1+10%)×140% / [ (1+10%)×140% + (1+0%)×(-40%) ] = 135.1%
För att åtgärda detta behöver den tillgång som gått bäst köpas och den tillgång som gått sämst säljas. Om aktier har går bättre än obligationer kommer investeringsstrategin att köpa aktier och sälja obligationer (låna mer pengar). Om å andra sidan aktier har gått sämre än obligationer kommer investeringsstrategin att sälja aktier och köpa obligationer (återbetala lånet).
Investeringsstrategin kommer alltså hela tiden köpa den tillgång som relativt sett är ”billigast” och köpa den som är ”dyrast”. En strategi som handlar på detta sätt kommer konsekvent att förlora pengar eftersom den ”köper dyrt” och ”säljer billigt” och detta ger en “volatilitetsförlust”.
Om det kommer uppstå en volatilitetsförlust eller volatilitetsvinst beror på exponeringens storlek. För alla portföljer med en exponering w mellan 0 och 100 procent kommer strategin leda till en volatilitetvinst medan den
för för alla andra portföljer kommer ge en volatilitetsförlust.
Sambandet kvantifieras på det som jag tidigare kallade ”gammat” och som beräknas som -w×(w-1). Ju mer negativt gammat är, desto större blir volatilitetsförlusterna.
Om den realiserade volatiliteten är v kommer volatilitetsförlusterna (“VF”) i en strategi med exponeringen w per år att vara
VF = exp( -0.5×w×(w-1)×v^2 ) - 1.
För måttlig hävstång (och volatilitet) kan ovan uttryck approximeras med
VF = -0.5×w×(w-1)×v^2.
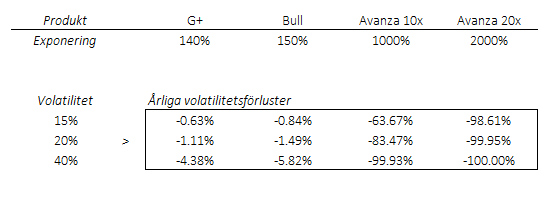
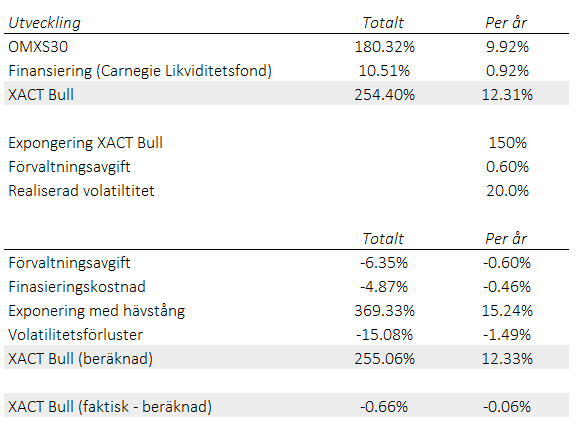
Om den realiserade volatiliteten är 15 procent och exponeringen 140 procent blir de förväntande volatilitetsförlusterna lika med 0.63 procent per år (till detta ska läggas trendavkastningen som alltid är positiv). Volatilitetsförlusterna i detta exempel approximeras alltså som
VF = -0.5×140%×40%×(15%)^2 = -0.63%.
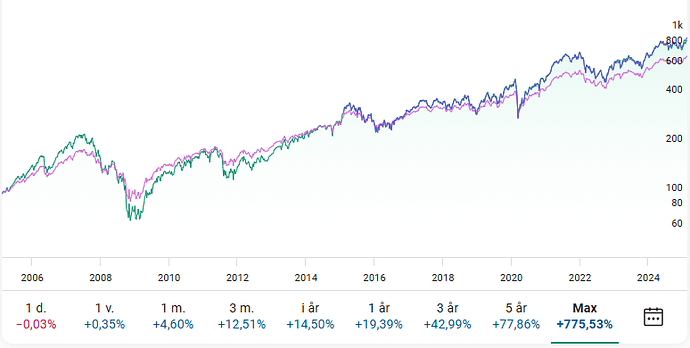
Detta kan kanske uppfattas som mycket. Det är dock viktigt att förstå att magnituden är en helt annan än i exempelvis de produkter med exponeringen på 10 eller 20 gånger som förekommer i börhandlade produkter och som jag hänvisat till tidigare. Se tabell nedan.
Nedan följer en förenklad härledning av dessa volatilitetsförluster (det kallas ”volatility drag” (som @zino med flera korrekt kommenterat redan) i en investeringsstrategi med hävstången w. Jag har försökt göra beräkningarna så begripliga som möjligt och har avsiktligt gjort vissa förenklingar som en teoretisk matematiker sannolikt skulle ha invändningar på.
På temat passar jag också på att svara på frågan från ”Preppern” gällande skillnaden mellan daglig och månatlig omviktning. Det är en mycket klok fundering. Jag var för något år sedan själv tvungen att lägga lite tid på att reda ut detta efter att just samma fråga ställts av ett försäkringsbolag.
Svaret är att daglig omviktning historiskt, för den typ av “måttlig” hävstång som vi använder, varit bättre även om detta innebär en mer frekvent ombalasering. Det har inte att göra med att transaktionskostnaderna blir större utan beror, lite förenklat, på att den dagligt obalanserade strategin, i en aktiemarknad som går upp, kommer att ha högre genomsnittlig exponering mot marknaden och därmed bättre avkastning. Om jag kommer ihåg rätt är dock den historiska skillnaden i avkastning marginell och i storleksordningen 0.15 procent per år.
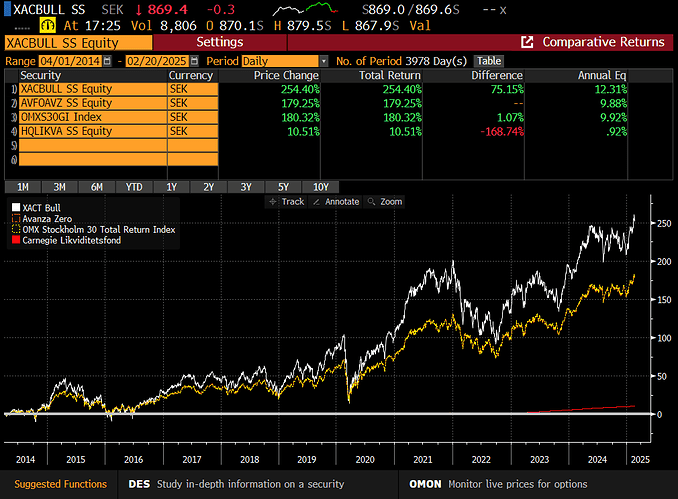
I Bull och Global Plus tillämpar vi en lite annorlunda ansats där vi tillåter exponeringen variera i ett spann som är 10 procentenheter brett. Vår slutsats (detta får bli vid behov bli föremål för ett ytterligare svar) är att fonderna genom detta reducerar såväl volatilitetsförluster som transaktionskostnader samtidigt som fonden effektivare kommer kunna hantera in- och utflöden.
![]()