Bakgrund
Detta är en spinoff på en tråd skapad av @janbolmeson där vi diskuterade hur mycket guld som skall finnas i en portfölj:
Diskussionen tog en vändning då @axr, @ludde35711, @Skrivkramp, @Anonym och jag själv började diskutera huruvida guld verkligen är bättre än räntor ur risk/avkastning-synpunkt. @axr hävdade att den effektiva marknadsportföljen som följer en optimering av Sharpe-kvoten har en fördelning mestadels bestående av räntor och aktier, och att guldet endast har en marginell effekt. Jag själv hävdade att guld var bättre än räntor då det gav en lägre risk med bibehållen avkastning om risk defineras som maximal förlust–engelskans maximum drawdown (MAD)–istället för standardavvikelse som vid Sharpe-kvotoptimeringen.
I hopp om att bevisa att jag hade rätt så körde jag en optimering där jag minimerade den maximala förlusten för att hitta den bästa portföljkonstellationen bestående av aktier, räntor och guld. Det visade sig att min tes om att guld ger lägre MAD än räntor med bibehållen avkastning var fel!
Syfte med denna tråd
Denna tråd ämnar att diskutera de förvånande resultaten vi såg efter minimeringen av den maximala förlusten. För att åstadkomma det så har jag gjort två optimeringar; en som minimerar MAD och en som maximerar Sharpe-kvoten. Att maximera Sharpe-kvoten är det man brukar kalla för “tangency portfolio” i vanlig portföljoptimering på den effektiva fronten. Denna gång har jag använt det eminenta vertyget PortfolioVisualizer som @axr introducerade för mig. Det gör i stort sett samma sak som själv hade gjort, så varför återuppfinna hjulet?
Resultaten från optimeringarna kan ses i denna PDF.
Jag kommer däremot presentera några highlights här för båda portföljerna. De tillgångsslag jag använt vid båda optimeringarna är följande:
- Amerikanska aktiemarknaden
- Långa treasury bonds
- Korta treasury bonds
- Guld
Data sedan 1978 har använts.
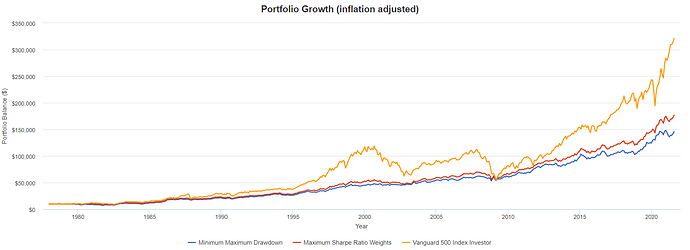
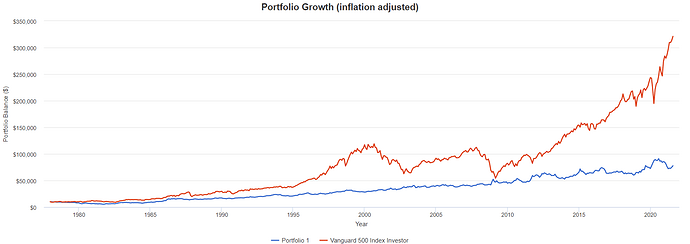
Minimera Maximala Förlusten
Den optimala portföljkonstellationen är i detta fall följande:
- Aktier: 10.4%
- Långa räntor: 0.0%
- Korta räntor: 89.6%
- Guld: 0.0%
Några nyckeltal är följande:
- Maximum drawdown: -3.59%
- Medelavkastning: 6.61%
- Standardavvikelse: 3.26%
- Sharpe-kvot: 0.64
- Beta: 0.12
- Skewness: 1.40
Maximera Sharpe-kvoten
Den optimala portföljkonstellationen är i detta fall följande:
- Aktier: 23.2%
- Långa räntor: 11.1%
- Korta räntor: 62.7%
- Guld: 3.0%
Några nyckeltal är följande:
- Maximum drawdown: -9.09%
- Medelavkastning: 7.96%
- Standardavvikelse: 7.79%
- Sharpe-kvot: 0.70
- Beta: 0.25
- Skewness: 0.39
Marknaden som benchmark
Några nyckeltal för den amerikanska aktiemarknaden är följande:
- Maximum drawdown: -50.97%
- Medelavkastning: 13.29%
- Standardavvikelse: 15.02%
- Sharpe-kvot: 0.54
- Beta: 1.00
- Skewness: -0.63
Diskussion
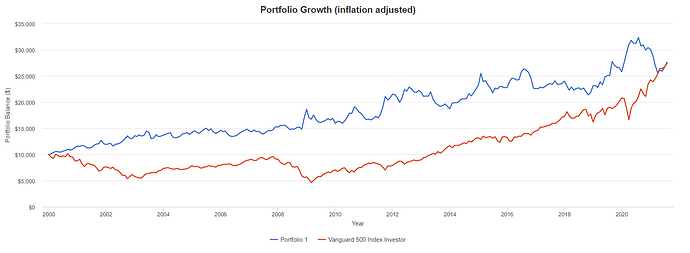
Att minimera den maximala förlusten leder till en mycket intressant portföljkonstellation med korta räntor och aktier. Den har en extremt låg MAD, vilket är förväntat. Men det har också förvånansvärt hö medelavkastning och även hög Sharpe-kvot. Detta tyder på att vi kkan motivera en relativt hög belåning på denna portfölj och på så vis få en avkastning i linje med marknaden som helhet utan att ta en alltför stor risk.
Problemet är då hur belåningen kan motiveras rent ekonomiskt. Om vi bekpnar en portfölj huvusakligen bestående av räntefonder så går vi både lång och kort i ränteläget!
- Vad är era tankar om resultaten av dessa portföljoptimeringar?
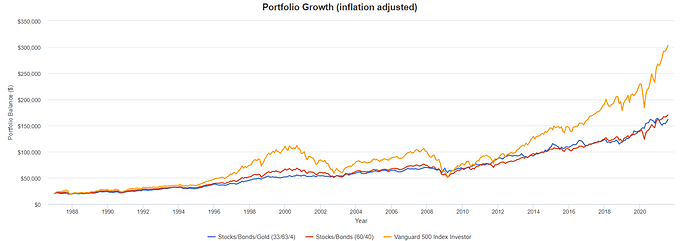
- Är det rentav bättre att ha en portfölj med korta räntor, lite aktier och belåna den än den klassiska 60/40-portföljen?
- Är guld kanske överflödigt ur risksynpunkt i en portfölj med tanke på vad dessa optimeringsresultat visar?