Jag uppfattar det som att metoderna som @PHans och Magiullis använder skiljer sig något.
Som jag förstått gör @phans ETT köp när gränsen till dippen nåtts medan Magiullis vid samma gräns dels köper för allt sparat OCH fortsätter månadköpa tills föregående topp åter nåtts.
Slutsatsen kan ju dock vara densamma.
Ja, det är en liten skillnad i strategi men den skillnaden är liten i jämförelse med hur tidsaspekten hanteras (och troligtvis till fördel för Nicks strategi i medel med tanke på att börsen tenderar att gå upp).
Ja det är såklart att “the great dep” å WW2 blir väldigt utslagsgivande. Det var därför jag tog ett andra exempel från 50-talet. Tycker dock fortfarande det kan vara relevant att även titta på ett case där “the great dep” finns med. Det har ju faktiskt inträffat och skulle kunna hända igen. Det innebär i princip att man bygger sin portfölj map en “100 year storm”.
Det är intressant att titta på alla tänkbara 20-årsperioder men skulle säga att sannolikheten att överprestera med den ena eller den andra inte ger hela bilden (dvs 3 av 4 gånger). Du kan ju t ex spela 34 nummer på roulette 100 gånger vilket gör att kommer vinna ca 90 gånger och förlora 10 gånger. Nu visar iofs grafen @econ101 delade att skillnaden tenderar att bli större när “Buy the Dip” underpresterar vilket snarare borde förstärka effekten. Så det rimmar väldigt dåligt med mina beräkningar.
Magiullis specificerar inte vilken data han använt (går säkert att hitta via git-länken) mer än att det är US Stocks. Sen använder han ju inte inflationsjusterade insättningar (jag tänker månadsspar t ex 10% av lönen) men borde kanske bli ungefär samma effekt för båda strategierna.
Nu har jag gjort det här i excel så det blev mycket handpåläggning men ska uppdatera med ett python-script så det enkelt går att titta på olika tröskelvärde och tidsperioder.
Som jag nämnde i förra inlägget så hade det varit intressant att få med den “riskfria räntan” till fördel för “Buy the Dip” i kalkylen (tänk bästa rörliga bankkontoräntan på olåsta pengar). Nån som har koll på vilken data som skulle va relevant att använda?
Jag tror du missat själva huvudpoängen med mitt inlägg, den finns även med i Nick’s dataset och i flera av utfallen som histogram avser.
Självklart måste man ta hänsyn till hur pass stor effekten är när man överpresterar resp. underpresterar.
Precis därför jag är skeptisk till att lägga för mycket vikt på dina resultat då de troligtvis härförs till extrema rörelser i svansen på en fördelning. Det vill säga skillnaden som uppstår (givet att du räknat rätt) domineras av extremt ovanliga händelser som inte är speciellt sannolika inom en normal investeringshorisont. Därmed blir dessa inte representativa för vad som är mest troligt utan endast vad som är det absolut bästa resultatet till fördel för “torrt krut”. Samt igen vill jag poängtera att även rullande X års horisonter (välj X så det blir relevant för specifik sparhorisont) tar hänsyn till de värsta tidsperioderna.
Jodå det gör han, både länk till data samt specifika intervall finns i artikeln.
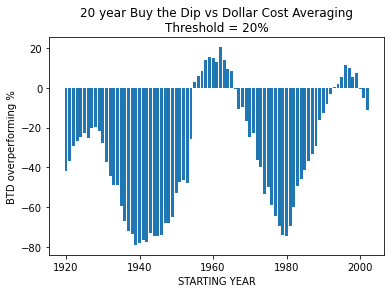
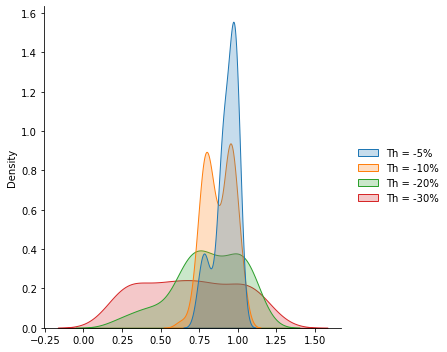
Jag lägger mig platt här. Har gjort om beräkningen i python och det hade smugit sig in ett “litet fel” i excelarket. Nu stämmer det ganska väl med Magiullis trots att strategin inte är exakt densamma. Även med 3 month Treasure Bill (riskfri ränta) så är det tveklöst bättre med månadsspar (DCA).
Sorry for the inconvenience! ![]()
Beröm till tråden för bra diskussion och @PHans snygga tvärvändning. ![]()