Hur är det @Anonym, och ursäkta min okunskap: Man kan inte sätta schablon inköpspris på fonder (1/5), så att maximal skatt blir 24% av försäljningssumman?
2 gillningar
24% på realiseringen, dvs 1.92% på kapitalet om 8% realiseras, motsvarande schablonintäkt på 6.4%.
2 gillningar
Det kan jag inte och efter sista turerna i tråden så ser man tydligt hur knasigt det lätt blir.
Hursomhelst, jag köper att det kanske vore en poäng att i uttagsfasen flytta till fondkonto för att minska just SoR-risken, men då kanske primärt några års uttag och då är det, som jag ser det, nog lika bra att ha den summan på ett bankkonto med ränta. Har man inte heller något att kvitta en förlust mot så blir det också mindre intressant.
Så jag stannar vid min plan med ISK och 2-3 årsutgifter på löpande fasträntekonton.
9 gillningar
Ja, det lutar åt kvartalsuttag och samtidig balansering baserad på förutbestämda nivåer. Jag tror det ska ge en lagom smidig hantering av vardagspengarna.
1 gillning
Jag hade valt ISK endast i ett scenario. Om jag visste 100% att jag för all framtid (dvs portföljens framtid, inte bara min) endast kommer att realisera kapital med svensk skattehemvist.
Om denna förutsättning inte gäller så är det fel att jämföra med AF skatt på 30%.
Om man dock är säker på denna förutsättning om framtiden så är ISK “minst dåligt”. 
Ja, uttagstiden är ytterligare en aspekt. Har börsen stigit kraftigt under säg 5 år och man vet att man skall lyfta sina pengar under några få år, då kan jag förstå om en flytt från ISK känns lockande.
I mitt fall känns det som halva ISK finns kvar när jag dör, och vilka variabler man använder, så verkar ISK vara bäst.
2 gillningar
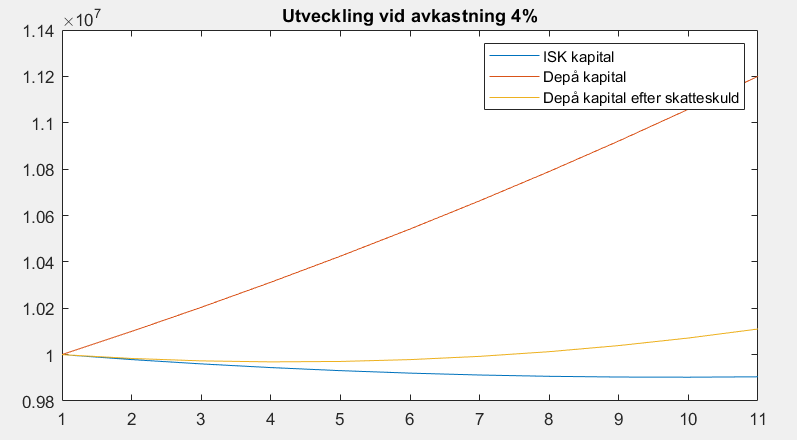
Yes det beror helt klart på hur man räknar och förutsättningarna. Vid 8% avkastning och uttag på ca 8% blir det klar favör ISK. Räknar man på en nedgång följt av lite surare börs men ändå en snittavkastning på +4% över 10år men ett uttag istället på 300K och att ISK skatten är på 1,2% blir det nedan diff:
| Exempel med 4% avkastning , startkap 10MSEK uttag 300K. Skatt på ISK 1,2% | AF | ISK |
|---|---|---|
| År 1 säljs 300 KSEK, våra andelar är nu värda 1 040 SEK styck. Skatten blir 300 x (1040/1000 -1) x 0,3 = 3600kr | 3 600 kr | 120 000 kr |
| År 2 säljs 300 KSEK, våra andelar är nu värda 1 081,6 SEK styck. Skatten blir 300 x (1081,6/1000 -1) x 0,3 = 7344kr | 7 344 kr | 120 000 kr |
| År 3 säljs 300 KSEK, våra andelar är nu värda 1 124,9 SEK styck. Skatten blir 300 x (1124,9,6/1000 -1) x 0,3 = 11238kr | 11 238 kr | 120 000 kr |
| År 4 | 15 287 kr | 120 000 kr |
| År 5 | 19 499 kr | 120 000 kr |
| År 6 | 23 879 kr | 120 000 kr |
| År 7 | 28 434 kr | 120 000 kr |
| År 8 | 33 171 kr | 120 000 kr |
| År 9 | 38 098 kr | 120 000 kr |
| År 10 | 43 222 kr | 120 000 kr |
| Summa: | 223 772 kr | 1 200 000 kr |
| Diff: | -976 228 kr |
Blir ändå en skattediff på nästan 10% av initialt kapital vid uppåtgående (om än måttligt) börs. Så nåt att ha med sig ändå tycker jag. Skulle kunna resultera i att man gör analysen att sätta in de sista 3-5 åren man annars hade placerat i ISK i vanlig AF istället tex.
Tillägg: Lät isk skatten teoretiskt nollas mot avkastningen som inte tas ut för att hålla kalkylen enkel då det ändå bara är exempelsiffror.
2 gillningar
Risk för att jag har missuppfattat något riktigt rejält, men du kan ju inte ha samma ISK-skatt hela tiden? Med 4% avkastning och 300 k uttag ökar ju värdet av ISK med minst 100 000 kr per år…
2 gillningar
Gick inte så detaljerat här utan ville mest ge ett alternativ till beräkningen längre upp i tråden. Så för att hålla exemplet enkelt tänkte jag att det går ca på ett ut med skatten 120k ner och avkastning kvar 100k upp. Jag kan förtydliga det med en rad.
Fel i matematiken här. Du använder skattesatsen 0.3((1+0.04)^N-1) efter N år. Det ska vara 0.3(1-(1+0.04)^{-N}). Du ser att det är fel ganska enkelt genom att notera att din skattesats kommer bli större än 100% efter ett tag. Titta t.ex på fallet att kapitalet dubblerats, enligt din beräkning blir då skattesatsen 0.3(2-1) dvs 30%. När kapitalet har dubblerats är hälften av försäljningen vinst, dvs skatten på varje såld krona blir 0.3(1-1/2).
Formeln kommer ifrån att om 1 krona växer till (1+r)^N och du säljer allt så kommer du betala skatten 0.3((1+r)^N-1) vilket betyder att skatten på varje såld krona är 0.3((1+r)^N-1)/(1+r)^N vilket förkortas till uttrycket ovan.
1 gillning
Kan det vara så enkelt att så länge man inte tar ut pengsr är förmodligen ISK bäst? När man börjar ta ut och skall lyfta hela kapitalet på exempelvis 10 - 15 år talar mycket för att ett konventionellt sparande kan vara bäst, eller…
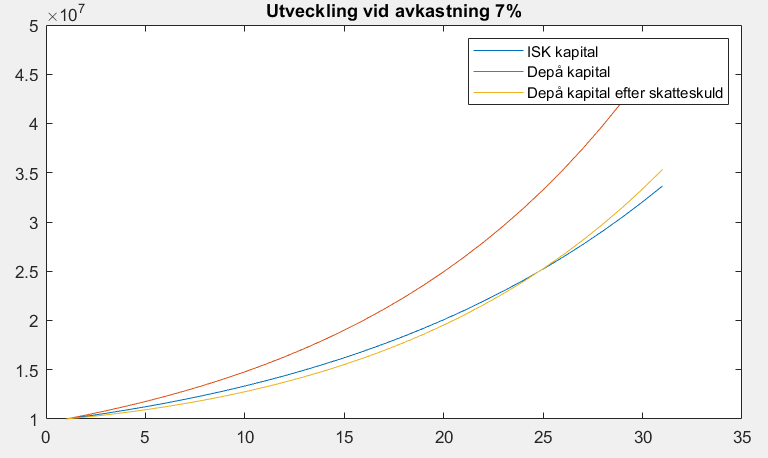
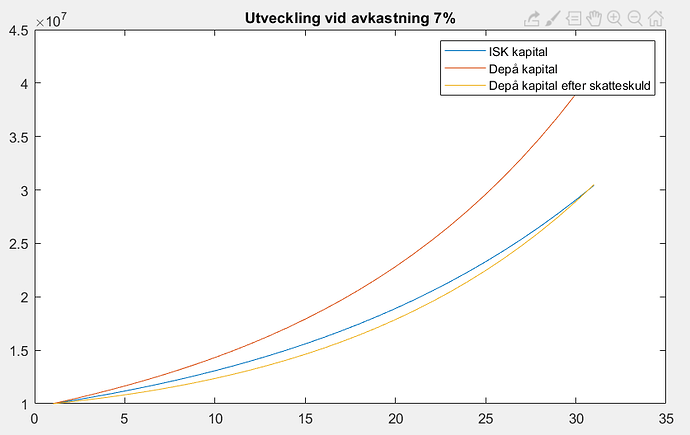
I det specifika exemplet, efter korrigering av felaktig matematik samt omgjord så att de är jämförbara så att man har lika mycket i näven efter uttag och betald skatt, så är det ungefär där brytpunkten ligger i att man har mer pengar på depån efter 10 år även efter latent skatteskuld.
Med lite högre avkastning skulle ISK-kapitalet vara större än depåkapitalet (efter skatteskuld) efter 10 år. Då kan man intuitivt tro att det betyder att det förblir så, men detta exempel är bedrägligt till viss del, eftersom uttagets storlek minskar relativt kapitalet. Om man då gör en asymptotisk analys så inser man att depån kommer växa sig större än ISK även efter latent skatteskuld efter tillräckligt många år (förenklat, om vi har avkastning r_A och skatt på ISK r_{ISK} så kommer kapitalet i depån efter tillräckligt lång tid i stort sett vara 100% vinst vilket betyder att 70% av värdet behålls, och då kapitalet växt så pass att uttaget för konsumtion kan försummas så betyder det att depån växer förbi då .7(1+r_A)^N > (1+r_A-r_{ISK})^N vilket ger uppskattningen N > \frac{\log(1/0.7)}{\log(1+r_A)-\log(1+r_A-r_{ISK}}). Används avkastningen 7% så ger formeln uppskattningen 32 år, och simulering visar att det sker efter ungefär 25 (det går lite snabbare eftersom skatten på depån är lägre än asymptotiska skatten, vilket tar ut effekten av att formeln försummar uttagen)
results = [];
rISK = 0.3*0.04;
rReturn = 0.04;
Wdep = 1e7;
Wdepreal = 1e7;
Wisk = 1e7;
totalGain = 1;
WithDraw = 300000;
totalTaxDep = 0;
totalTaxISK = 0;
for i = 1:20
Wdep = [Wdep Wdep(end)*(1+rReturn)-WithDraw];
totalGain = totalGain*(1+rReturn);
taxDep = WithDraw*0.3*(1-1/totalGain);
InHand = WithDraw - taxDep;
Wisk = [Wisk Wisk(end)*(1+rReturn)];
taxISK = Wisk(end)*rISK;
WithDrawISK = InHand + taxISK;
Wisk(end) = Wisk(end) - WithDrawISK;
Wdepreal = [Wdepreal Wdep(end) - 0.3*Wdep(end)*(1-1/totalGain)];
end
plot([Wisk' Wdep' Wdepreal']);axis([0 11 9e6 13e6]);legend('ISK kapital','Depå kapital','Depå kapital efter skatteskuld')
2 gillningar
Haha galet vad du räknar på 
Jag tänkte slänga in att efter 10år bör rätt skattesumma AF vara 179 560kr eftersom som du säger skatten kan inte på sikt bli över 30%x100% så det var nåt formelfel jag fick med mig vid copy. Men det ger alltså en positiv effekt till fördel AF. Om än ganska marginell på 10år mot 10MSEK så blir det ju stor skillnad på längre sikt. Men efter 10 år drygt 1Mkr bättre skattemässigt AF än ISK istället för knappt 1Mkr bättre.
Slutsatsen kvarstår att det i korta loppet kan vara intressant för att minska påverkan för tuff marknadstajming i början av en FIRE fas.
@Anonym Jag tänker att det påverkar genom att du i ISK caset allt annat lika behöver sälja fler fondandelar än AF caset eftersom du utöver ditt uttag behöver sälja fonder för att finansiera skatten. När marknaden sen fortsätter uppåt halkar ISK då efter. Särskilt om vi räknar med faktisk nedgång några år i början. Då har du uttag + ISK skatt att sälja andelar för medans AF bara har uttaget att sälja av för.
Du kan inte blunda för den latenta skatteskulden som ligger på depån. Staten har i praktiken en fodran på en betydande andel och lånar ut detta kapital till dig tills vidare. Det summerar till runt en miljon så skattemässigt är båda fallen ungefär lika efter 10 år.
Jag säger inte att jag blundar för den, tyckte bara det behövdes lite nyanserad balansering med ett exempel som inte var 8% avkastning och 800k i uttag. För att visa på att det kan finnas en poäng i en strategi som håller ner skatten initialt vilket kan rädda en FIRE-plan som är skör i inledningen men trygg efter 10år tex. Genom att inte behöva sälja av andelar för att betala skatt ovanpå uttagen.
Ett tydligare exempel blir det vid en nedgång på 15% år 1, stillastående börs kommande 4 åren och sen uppgång 5% per år i 5 år. Det skulle kunna vara ett sånt scenario man väljer att begränsa nedsidan i med ett AF konto. Det finns därefter en latent skatteskuld på AF kontot på ca 3% medans ISK kontot redan betalt ca 12% och sålt fler fondandelar till lågt pris för att finansiera skatten och därmed missar del av uppgången sista 5 åren.
Vilken beräkning pratar du om nu? Tråden startade med ett scenario där 8% plockades ut årligen. Det senare exemplet idag som simuleras några poster upp är åt helt andra hållet där någon funderade på ett fixt uttag på 300’000 från depån.
Beräkningen är gjord så att uttag är jämförbara i köpkraft. När 300’000 tas ut första året från depån så betalas 3460 kronor i skatt vilker ger 296540 kronor att spendera. För att ISK-innehavaren ska få lika mycket att spendera görs ett uttag på 296540 + 124800.
Jag visar inget särskilt, jag visar bara vad korrekta siffrorna blir i det exemplet som det gjordes en felaktig tabell för. I det senare exemplet togs kapital ut, men enbart 300’000 brutto.
Är det någon specifik uttagslogik du vill se data för? Här är situationen att 300’000 tas ut till konsumtion (dvs man tar 300’000 + skatt som behövs för att täcka vinstskatt på det man tar ut respektive skatt på schablonintäkt, avkastning 7% samt 0.12% extra belasting på depån).
Om du vill ha en uttagstrategi som är procentuell av kapital så blir det inte självklart hur man jämför, eftersom om depåstorlekarna utvecklar sig olika vilket gör att uttagen blir olika stora.
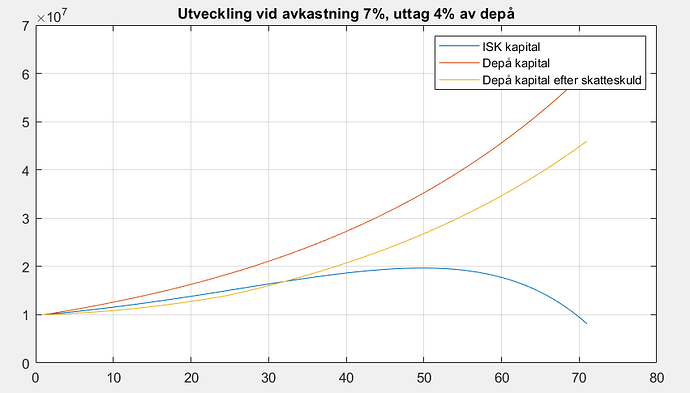
Här en variant där Jonny och Jenny sätter samma kapital i depå resp. ISK. Jonny tar ut 4% av sitt kapital och betalar skatt, och Jenny tittar på hur mycket Jonny hade kvar att konsumera för efter betald skatt och tar ut samma plus pengar till sin skatt.
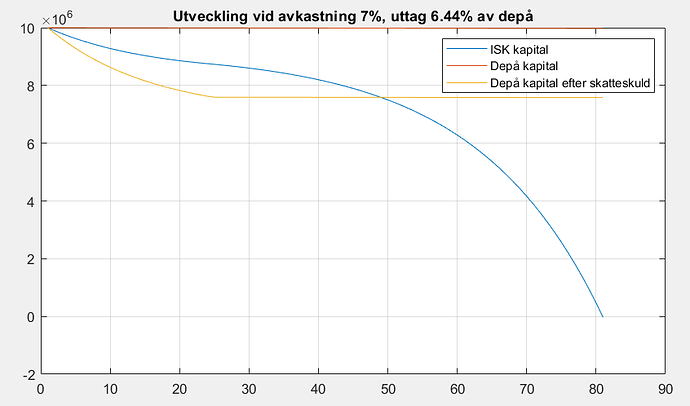
Nu börjar det hända intressanta saker. Eftersom uttaget är modest relativt avkastningen så kommer kapitalet växa och med tiden kommer depån bli större. Men lustigt nog så vänder Jennys kapital ner. Anledningen är att Jonny fortsätter plocka ut 4% av sin stora växande depå (innehållandes av staten till stora delar lånade pengar). Han har dock passerat gränsen för schablonbeskattning, så nu sjunker skatten och han får till slut kvar 76% av uttaget till konsumtion. Jenny som ska leva lika gott som Jonny måste således ta ut 76% av 4% av Jonnys depåstorlek för sin konsumtion för att få samma ekonomi, plus pengarna till sin skatt. Efter 50 år är Jonnys depå 1.8 ggr så stor som Jennys vilket betyder att hennes konsumtionsuttag är 0.04\cdot0.76\cdot 1.8 = 5.44% vilket med skatten blir 6.44% uttag, och eftersom (1+0.07)(1-0.0644) < 1 så börjar kapitalet minska.
Nu är Jonny mer aggresiv men siktar på att behålla kapitalet och tar ut 6.44% (vilket med schablonskatten betyder att kapitalet hålls konstant ty (1+0.07-0.0012)(1-0.0644)=1. Initialt sjunker verkligt kapital efter betald skatteskuld, men när schablonbeskattningsläget inträffar så stabiliserar sig depåns värde. Jennys ISK håller sig länge ovanför, men även här förlorar hon asymptotiskt.
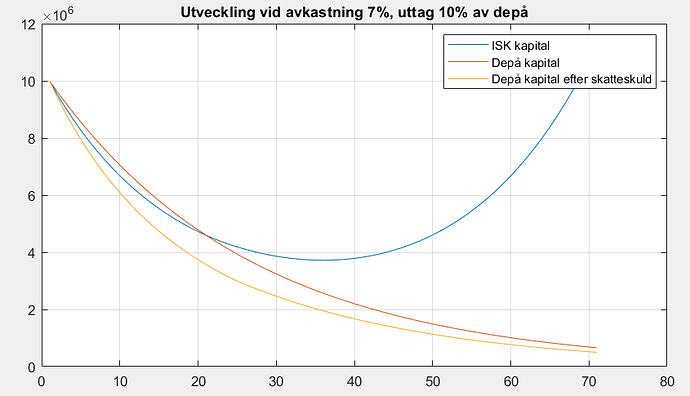
Slutligen ett exempel med aggresivt uttag av Jonny. Han plockar nu ut 10% av depåvärdet, och dränerar snabbt sitt kapital. Nu ser Jennys ISK helt magisk ut, men det är egentligen bara en effekt av att vi låst uttagsstorleken till Jonny referens, så när hans kapital minskar så tas en allt mindre absolut summa pengar ut, och efter ett tag blir uttaget försumbart i Jennys ISK och den växer med avkastningen.
Det tål att påminnas att procentuellt uttag av depå inte är rimligt, då det typiskt leder till drastiskt minskande eller ökande uttag.
6 gillningar
Det sparas inte i 35 år i desa exempel. Det är exempel med fast uttag (300k innan skatt repektive 300k efter skatt) samt med procentuellt uttag (4% så att det växer,6.44% så att det hålls konstant, 10% så att det sjunker) alla från dag 1.
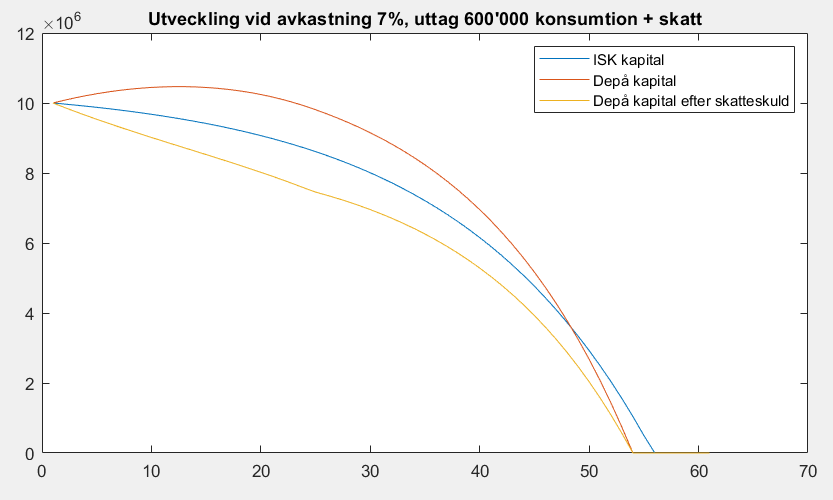
Här är ett till, 600’000 för konsumtion + skatt.
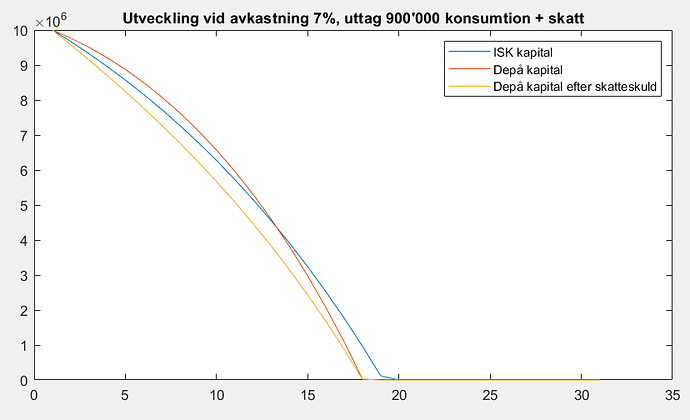
och ännu aggresivare, 900’000 + skatt (orimligt högt uttag, inget som skulle göras i praktiken med verklig avkastning)
1 gillning
Tycker visst det kan vara intressant med alternativa beräkningar som frångår TS initiala exempel. Annars blir det väl inte mycket till forum om vi alla bara ska stanna där i tanken. Känns som flera tagit sig en funderare på AF som alternativ för att minska risken i en initial uttagsstrategi.
För någon kanske det väger över att de kan räkna med en trygg FIRE nåt år tidigare än annars.
Vid 8% konstant uppgång ser många planer bra ut 
bra att utmana lite 
1 gillning
Siffrorna för ISK ser ut att stämma (förutom att du verkar använt en avrundad siffra som indata någonstans. Baklängesräknar jag så kan jag dra slutsatsen att du gör i ordningen kapitalisera, uttag (dvs första uttaget görs i december år 0). Då ska ISK år 1 börja med 10^7(1+0.08) - 800000 - 0.3\cdot0.04\cdot 10^7(1+0.08) = 9870400 vilket verkar stämma med din 9’860’000 om du avrundat någon siffra)
AFK ser dock ut att ha gått fel då de långsamt divergerar. Du är välkommen att finna skillnaden i antagande i koden nedan eller än bättre posta din kod som du använt för att generera din tabell
Vi kan dock se att något är vajsing i dina siffror. Om vi tittar på år 15 till 16 så har du här ingång 4’871’000. På 16 år har avkastningen varit 1.08^{16} vilket betyder att skatten på uttagen krona blir 0.3(1 - 1/(1.08^{16})) vilket är 21.24%. Vi måste ta ut för att täcka omkostnaden 800’000 samt schablonskatten på 0.12% av ingående kapital. Uttag som krävs är alltså (800000 + 0.0012\cdot 4871000)/(1-0.214). Kvar i december när kapitalet växt och det gjorts uttag är alltså 4871000\cdot 1.08 - ((800000 + 0.0012 \cdot 4871000)/(1-0.214)) vilket blir 4’237’500 medan din nästa rad indikerar ett uttag på 48’000 mer. Inte ens om jag använder schablonbeskattning på maximala 24% kommer man ner i 4189000.
Jag kan dock få väldigt nära dina siffror i varje steg om jag dubbelräknar schablonskatten, dvs både drar ner avkastning samt tar ut pengar för att betala den, samt använder en tiopotens fel när jag justerar avkastningen. Slump eller faktisk orsak vet jag inte då tabellen är avrundad vilket gör detaljanalysen svår.
Här är tabell för data genererad av koden nedan
Year AF ISK Tax
____ __________ __________ ________
0 1e+07 1e+07 0.022222
1 9.9695e+06 9.8704e+06 0.042798
2 9.9188e+06 9.7321e+06 0.06185
3 9.8469e+06 9.5846e+06 0.079491
4 9.7528e+06 9.4271e+06 0.095825
5 9.6352e+06 9.2591e+06 0.11095
6 9.4932e+06 9.0798e+06 0.12495
7 9.3254e+06 8.8885e+06 0.13792
8 9.1305e+06 8.6844e+06 0.14993
9 8.9069e+06 8.4666e+06 0.16104
10 8.6532e+06 8.2342e+06 0.17134
11 8.3675e+06 7.9863e+06 0.18087
12 8.048e+06 7.7216e+06 0.18969
13 7.6927e+06 7.4393e+06 0.19786
14 7.2992e+06 7.138e+06 0.20543
15 6.8653e+06 6.8166e+06 0.21243
16 6.3883e+06 6.4736e+06 0.21892
17 5.8653e+06 6.1075e+06 0.22493
18 5.2933e+06 5.717e+06 0.23049
19 4.6689e+06 5.3003e+06 0.23564
20 3.9885e+06 4.8556e+06 0.23564
results = [];
rISK = 0.3*0.04;
rReturn = 0.07;
rSchablon = 0.4/100;
Wdep = 1e7;
Wdepreal = 1e7;
Wisk = 1e7;
totalGain = 1;
Expense = 900000;
totalTaxDep = 0;
totalTaxISK = 0;
for i = 1:20
% Capitalize during the year
Wdep = [Wdep Wdep(end)*(1+rReturn)];
totalGain = totalGain*(1+rReturn);
taxRate = min(0.24,0.3*(1-1/totalGain));
% Cover expenses + schablon tax based on capital in january
WithDrawDep= (Expense + 0.3*rSchablon*Wdep(end-1))/(1-taxRate);
taxDep = WithDrawDep*taxRate;
Wdep(end) = max(Wdep(end) - WithDrawDep,0);
% Capitalize during the year
Wisk = [Wisk Wisk(end)*(1+rReturn)];
taxISK = Wisk(end)*rISK;
% Withdraw expenses + tax
WithDrawISK = Expense + taxISK;
Wisk(end) = max(0,Wisk(end) - WithDrawISK);
% Adjusted real wealth
Wdepreal = [Wdepreal Wdep(end) - Wdep(end)*taxRate];
end
plot([Wisk' Wdep' Wdepreal']);
title('Utveckling vid avkastning 8%, uttag 800''000 konsumtion + skatt')
legend('ISK kapital','Depå kapital','Depå kapital efter skatteskuld')
3 gillningar