Att skilja på procentuella och reella värdeförändringar

Övrigt
#1

Jag hör ofta påståenden som att

En nergång på 25% kräver en uppgång på 33% för att återhämta sig,
En nergång på 50% kräver en uppgång på 100% för att återhämta sig,
En nergång på 80% kräver en uppgång på 500% för att återhämta sig.

Jag hajar alltid till på detta, det man säger är naturligtvis rätt i sak, men frågan är om det egentligen är så relevant?

Det låter som att man implicit säger att det krävs en större värdeökning än värdeminskningen för att fullborda återhämtningen, vilket å andra sidan inte är rätt i sak.

Exempel:

Du har 100kr, och köper en bok för 50kr.
Ditt kapital har nu minskat med 50%, till 50kr
Du säljer nu boken för 50kr.
Ditt kapital har nu ökat med 100%, till 10kr
Men att beskriva detta i procent är irrelevant, det enda som har skett är två transaktioner på 50kr.

Liknelsen fungerar även på börsen, tillgångarna på börsen har reella värden. Det är bara extremt opraktiskt att tala om och jämföra aktier, index och fonder i dess reella värden. Därför är det mer relevant att säga att en aktie värd X % mer eller mindre än igår.
Liksom det är mer relevant att OMX gått upp med 1%, snarare än 20 punkter

Exemplet ovan gäller lika mycket för ett bolag som har sett sitt börsvärde minska från 1 000 mkr till 200 mkr och sedan återhämtat sig på grund av {insert reason here}. Värdeförändringen i båda fallen är 800 mkr. Visst är det också sant att bolagets börsvärde fallit med 80% och sedan ökat med 500%, men det är ett lite vilseledande sätt då det får uppgången att låta som en mycket mer spektakulär händelse än nedgången.

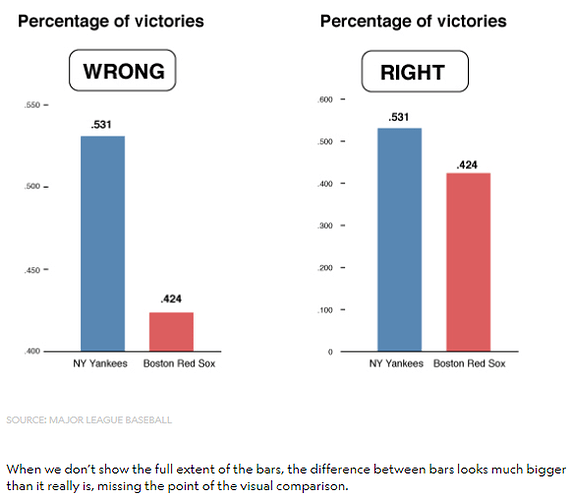
Se det lite som en medvetet eller omedvetet dåligt utformad graf där man satt skalan felaktigt och får det att se mer dramatiskt ut än det egentligen är

image
image582×509 31.5 KB

Jämförelsen med en dålig graf ligger också närmare procent-vs-värde-problematiken än man kan tro.

När man ser på förändringen i % på börsvärdet för det fiktiva bolaget ovan så använder man två olika referenspunkter när man säger att det först backar 80% och sedan stiger 500%, och det är där själva förvirringen ligger. I ena fallet utgår man från 1 000 mkr och räknar % från basvärdet 1 000 mkr. I andra fallet utgår man från 200 mkr och räknar % från basvärdet 200 mkr

Om vi har följande scenario

2020, börsvärde 1 000 mkr
2021, börsvärde 200 mkr
2022, börsvärde 1 000 mkr

Då är följande beskrivningar av ovan sjysta och sanna

  • Mellan 2020 och 2022 förändrades börsvärdet 0%
  • Börsvärdet minskade med 800 mkr mellan 2020 till 2021
  • Börsvärdet ökade med 800 mkr mellan 2021 till 2022

Följande beskrivning av ovan är lika sann men kan vara något vilseledande beroende på i vilken kontext man talar om det

  • Börsvärdet sjönk först med 80% mellan 2020 och 2021, för att sedan stiga med 500% året därpå

Det jag egentligen vill ha sagt, och jag hoppas jag fått fram, med detta kanske onödigt långa inlägg är att det är inte fel i sak att säga att en tillgång går ner x% och sedan återhämtar sig efter en uppgång på y%.
Men det är fel att argumentera att en nergång är dålig på grund av att det krävs en större uppgång än nergång. För det menar jag inte är sant.

@janbolmeson du bör känna dig träffad :innocent: :sweat_smile: :shushing_face:

15 gillningar
#2

Du har ju rätt i sak men det är väldigt opraktiskt att använda punkter eller kronor för de måste ju relatera till något för att få mening. Och då får man ändå räkna om det på något sätt.

Om de flesta tänker och agerar i procent är det bra att också göra det själv. Tycker många att 2% är en stor uppgång är man kanske inte lika köpsugen som om en uppgång bara är 0,25%. Oavsett priset.

Ett undantag kan vara om börsen faller 10% på kort tid. Då kan man kanske tycka att en tvåsiffrig uppgång direkt efter kan vara “normalt” i det läget.

Det är en akademisk och psykologisk fråga.

#3

Håller med dig till 100% ( :point_left: pun intended) här @nhb. Det är extremt opraktiskt att prata om rörelserna på börsen på något annat sätt än i procent, och jag tycker inte man ska göra detta på något annat vis.

Det jag motsäger mig lite är uttalanden som.
“Glöm inte att om börsen faller 50% måste den stiga 100% för att återhämta sig”
Då man använder skillnaden i procent för en och samma värdeförändring, som ett argument för hur illa det skulle vara med en värdeminskning på 50%.
Som om en tillgång du ägers värde halverades inte vore illa nog :sweat_smile:

2 gillningar
#4

Det är väl för att man förväntar sig att en viss procentuell uppgång är det normala. Dessutom är det extra tufft efter ett ras eftersom varje procent då är mycket mindre värd i kronor.

#5

Ja men det är just detta jag egentligen är inne på. Eftersom man bytt basvärde/ utgångspunkt/ tittar ur ett annat tidsperspektiv, så jämför man inte äpplen med äpplen längre.
Att det är “färre kronor per procent” efter en nedgång stämmer bara eftersom man utgår från tillgångens nya värde.

Exempel.

2020-01-01 - 2020-03-23 gick OMX30 -27,07%
2020-03-24 - 2020-12-31 gick OMX30 +45,07%
Men helåret…
2020-01-01 - 2020-12-31 gick OMX30 +14,63%

Ovan beskriver båda hur året 2020 gick, men när man tittar på det i procent är det svårt att intuitivt förstå att -27,07% + 45,07% = +14,63%. Detta beror bland annat på att man helt byter referenspunkt och utgår från börsens relativt sett lågre värde när man beskriver uppgången från den 24:e mars till årskiftet.

Om jag istället skriver

2020-01-01 - 2020-03-23 minskade OMX30 med 516,36 punkter
2020-03-24 - 2020-12-31 ökade OMX30 med 582,47 punkter
Men helåret…
2020-01-01 - 2020-12-31 ökade OMX30 med 66,11 punkter

Då är det enkelt att förstå vad som hände på hela året genom att bara få de två första tidsangivelserna.
Först minska de det med 516,36 punkter, sedan ökade det med 582,47 punkter, totalt gick det upp med -516,36 + 582,47 = 66,11 punkter

Känner mig lite dum när jag försöker förklara detta, för jag tycker det är svårt att hitta orden för att beskriva det på ett bra sätt.
Det är viktigt att förstå att en uppgång på 10% inte återhämtar en tidigare nergång på 10%, och det förstår man ju när man säger att det krävs en uppgång på 100% för att hämta upp ett tapp på 50%. Men det är lika viktigt att förstå varför det är så

1 gillning
#6

Du har helt rätt. Men jag förstår inte riktigt din poäng.

#7

Poängen är att eftersom procentökningen som krävs för återhämtningen är större så skapar det illusionen att börsen måste arbeta hårdare för att komma tillbaka dit, vilket inte är fallet. Tar du hälften av en tårta så har tårtan tappat 50%. För att tårtan ska återhämta sig så måste den öka med hela 100%!!! Men om du sätter tillbaka samma bit som du tog så har den gjort det, det krävs inte mer arbete än det som gjordes när den blev mindre.

7 gillningar
#8

Jag tycker nog att börsen får arbeta hårdare för enligt min amatörmässiga notering går generellt sett nedgångarna tre gånger så snabbt som uppgångarna. Inte nog med att varje procent är mindre värd efter ett ras, det tar också mycket längre tid att komma tillbaka.

Men om jag tänker så som du föreslår, vad har jag för rationell nytta av det?

#9

Äntligen! Har i mitt stilla sinne undrat om det bara varit jag som tyckt det varit missvisande. Väl formulera.

2 gillningar
#10

Det kan vara så att börsen faktiskt måste arbeta hårdare för att återhämta ett visst fall, men anledningen till det är inte att procentökningen som krävs är högre än procentminskningen, utan en massvis av komplexa ekonomiska & psykologiska aspekter.

1 gillning
#11

Jag tycker det är en bra poäng av TS.
Man blir lätt lurad även om jag själv kan räkna procent.

#12

Exakt, det kan vara så att det är svårare att hämta in en förlust, åtminstone under vissa förutsättningar. Men det har inget som helst att göra med beskrivningen av upp- och nergång i procent.

1 gillning
#13

Ja, det är nog det jag tror är det svåra här. Uträkningen är ju inte ”fel”. Den används bara lite lättvindigt som ett argument för fel saker ibland.

#14

Anta att investerarna tappar förtroendet för en aktie och börjar handla ner den i enprocentssteg. Det tar då ungefär 69 steg för aktien att halveras i värde: 0.99^69 ≈ 50. Anta sedan att förtroendet för aktien ökar och investerarna istället börjar handla upp aktien i enprocentssteg. Slutvärdet kommer då vara (0.99*1.01)^69 ≈ 0.993, dvs nästan samma. Ett ytterligare steg (70 istället för 69) och värdet på aktien > det ursprungliga värdet. En nedgång med 50% är ganska extremt och effekten blir ännu mindre för låt oss säga 30% nedgång. Slutsatsen blir att uppgång/nedgång är i det närmaste symmetriska. Den matematiska effekten är försumbar.

1 gillning
#15

Intessant inlägg. Har inte tänkt på att det blir skillnad om man tittar på förändringen i inkrementella steg som du beskriver ovan.

Det du säger är att om ett företag tappt ca 1% om dagen i en månad, och sedan stiger 1% om dagen i en månad så är man tillbaka nära utgångsvärdet.

0,99^30 + 1,01^30 = 99,7% av ursprungsvärdet.

Man kan beskriva exakt samma skeende med att säga att företaget minskade i värde med 26% första månaden, sedan steg med med 34% månaden därpå.

Procent är förvirrande, eller hur :innocent:

#16

Det är ju också ett sätt att se det på! Vid varje krona är varje procent lika mycket värd oavsett om den är på väg upp eller ner. De tunga effekterna har vi i ändlägena, där vi börjar vår resa upp eller ner.

Men står vi där med -50% i bagaget är det ändå lång väg tillbaka. Jag vill inte hamna där.

1 gillning
#17

Jag har också undrat varför det här med 50% nedgång och 100% uppgång tas upp så ofta, det är ju faktiskt ganska intetsägande, ett slags trixande med procenträkning mot bättre vetande. Om man skippar procenten kan man också säga så här:

Tänk på att en halvering av ditt kapital kräver en dubblering för att du ska återhämta halveringen.

Jaha, har påven en lustig mössa?
Sover Dolly Parton på ryggen?

2 gillningar
#18

Samma sak när börsen rasar. Varje procent ner är värd färre kronor och anledningen att sälja, analogt med detta, borde successivt avta.

Slutsatsen att dra skulle då kunna vara att ska man sälja ska man göra det tidigt medan procenten är dyra och sedan också köpa tidigt medan procenten är billiga. Men eftersom uppgången i normalfallet oftast är långsammare i tid än nedgången får man längre tid på sig då. Vill man agera snabbt är det på säljsidan man ska göra det i första hand.

#19

Jag tror att många tycker att de säger något klokt och insiktsfullt när de upprepar detta. Det är därför det återkommer så ofta. Någon mer detaljerad analys brukar sällan följa. Om denna matematiska effekt inte var marginell skulle graferna över aktiekurser se helt annorlunda ut och i princip sakna V-formade uppgångar/nedgångar.

1 gillning
#20

Svårigheten ligger i att vid tillfällig nedgång så missar man uppåtrekylen om man går ur för snabbt. Man vet ju tyvärr inte på förhand hur länge och hur djup nedgången kommer att bli. Just för fonder blir det extra svårt i och med att man dessutom har flera dagars fördröjning då man är utanför marknaden och lätt hamnar i ofas vid byten.