Nej, ett konto som betalar ut oftare kommer förlora på ränteförändringar om man jämför två konton med samma effektiva ränta, oavsett om räntan höjs eller sänks.
Matematiskt för specifika fallet att vi har två konton som med samma initiala effektiva ränta r_1, där effektiva räntan sedan ändras till r_2 vid halvårsskiftet, så kommer den “effektiva effektiva” räntan på årsutdelande bara vara aritmetriska medelvärdet p_1 = \frac{r_1+r_2}{2} medan det konto som delar ut i halvårsskiftet kommer landa i den effektiva effektiva räntan p_2 = (1+r_1)^{1/2}(1+r_2)^{1/2}-1. Att p_1 > p_2 då p_1 \neq p_2 följer av en relation kring aritmetriska och geometriska medelvärden som sammanfattas i något som kort kallas AM-GM-olikheter.
Problemet med kontot med flera utbetalningar med samma effektiva ränta (men sålunda lägre nominell) är att den effektiva räntan blir just effektivt ekvivalent först i samband med den sista utbetalningen för året, och den effekten visar sig vara aktiv både vid sänkning och höjning, den ligger så att säga alltid lite efter men kommer ta igen det på målsnöret. När räntorna ändras flyttas snöret, och den förlorade nominella räntan dittills kan aldrig tas igen.
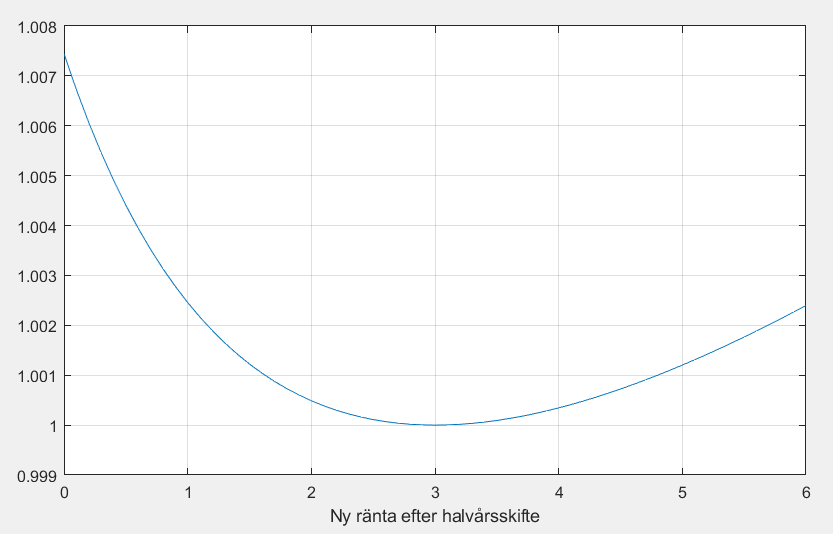
Vi kan t.ex titta på fallet med att två konton börjar med r_1 = 3\%, som sedan ändras till ny effektiv ränta r_2 från halvårsskiftet, där vi testar olika räntor från 0\% till 6\%, och sedan se på vad effektiva effektiva räntan blev vid helårsskiftet, dvs hur mycket pengar finns på de två kontona. Skillnaden är så oerhört liten vid relevanta räntenivåer så istället för att plotta de två effektiva effektiva räntorna (dvs formlerna ovan som skulle ge en rät linje för p_1 och en konkav linje p_2 precis under p_1 som sammanfaller vid 3\%) så plottar jag kvoten \frac{p_1}{p_2}.