Spitznagel skriver faktiskt om Kelly Criterion i Safe Haven också, och kommer fram till samma slutsats, dvs att betta ~40% av kapitalet per tärningskast är optimalt.
Jag har självt haft intuitivt svårt att förstå både Kelly och försäkringen, i båda fallen känns det nästan magiskt att avkastningen ökar när man lägger till något med noll förväntad avkastning.
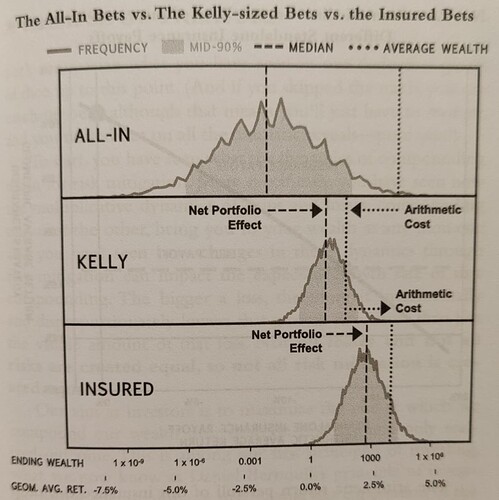
Ovanstående bild från boken gjorde dock mycket för min förståelse. Här har Spitznagel simulerat tusentals kast och plottat utfallen i en graf. Vi ser att:
-
All-in-strategin (betta 100% varje kast) har klart högst spridning av utfall, och klart högst aritmetiskt medelvärde (prickad linje), medan medianen (streckad linje) ligger lågt pga negativ geometrisk förväntad avkastning (-1,5% per tärningsslag, som konstaterats i tråden). Notera att skalan är logaritmisk, varför medelvärdet ligger så långt åt höger.
-
Kelly-strategin (betta ~40% varje kast) komprimerar utfallen. Aritmetiska medelvärdet sänks eftersom vi allokerar 60% av portföljen till cash, men medianen ökar pga positiv geometrisk förväntad avkastning (+0,64% per tärningsslag).
-
Försäkringsstrategin (försäkra med 9% varje kast) komprimerar utfallen, men flyttar också hela grafen åt höger. Detta eftersom aritmetiska medelvärdet inte sänks lika mycket eftersom majoriteten av portföljen ändå allokeras till bettet, och geometrisk förväntad avkastning ökar därmed ytterligare (+2,1% per tärningsslag).
För att göra en enkel liknelse kan vi ponera att hela jordens befolkning spelade detta bet. All-in-strategin hade statistiskt medfört högst förmögenhet i slutändan (mätt i total summa pengar i världen), men den hade varit koncentrerad till en liten andel snuskigt rika individer, medan majoriteten hade förlorat pengar. Kelly-strategin och försäkringsstrategin minskar den totala förmögenheten, men minskar också spridningen mellan individer och gör att nästan alla får en måttligt god avkastning istället.
Ovanstående resonemang är orsaken till att jag har valt att ha aktiva volatilitetsfonder i portföljen. De minskar chansen att bli snuskigt rik, men ökar chansen till en god och stabil avkastning.