Kanske en dum fråga, men blir det skillnad principiellt om man balanserar om genom
-
sälja andelar i fond x och köpa i fond y, eller
-
riktar nysparandet till endast fond y till dess man återfått balans.
Nja men det första alternativet går ju fortast och ombalanseringen är gjord på nån dag.
Alternativt 2 kan ju ta mycket lång tid om det är en portfölj med stort belopp. Under den tiden hinner dessutom portföljen fortsätta drifta.
Jag förstår tanken med att låta trenden spela ut lite mer och därför ombalansera lite mer sällan, t.ex en gång per år.
Menar du att just intervallet om c 12 är det viktiga för det är relaterat till hur långt trender brukar hålla i?
Skulle det hypotetiskt kunna vara längre än ett år? ( om man bortser från månadsflukationer).
Finns det data som stöder detta?
Tack!
Tack för klargörandet!
I mitt fall räcker det oftast med någon månad för att korrigera med riktat sparande så jag fortsätter så
Att det är bra att rebalansera sällan finns det studier som visat ex denna:
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2458618
Efter att ha många ggr ha letat studier om optimal rebalanserings frekvens och
efter att under flera år rebalanserat varje vecka började jag fundera över varför kan börsen stiga/falla 20-30% per år men jag aldrig läst om en enda metod för rebalansering som genererar samma positiva kursrörelser?
Rebalanserar man tidigt i en fallande marknad accelererar man sin förlust.
Säljer man tidigt i en stigande marknad minskar man sin vinst.
Det finns inga vetenskapliga studier om rebalansering som visat att rebalansering överträffar trenden.
Har ni sådana studier så läser jag dem gärna.
1 gillning
Från ovan paper
For percentage threshold-based policies, the superior (inferior) outcomes were associated with rebalancing only when portfolio weights were 5% or more (less than 5%) out of balance.
Från Vanguards paper som nämns längre upp i tråden.
Our strategists employed a framework for determining an ideal risk-return and cost-efficient rebalancing strategy. Our research shows that optimal rebalancing methods are neither too frequent, such as monthly or quarterly calendar-based methods, nor too infrequent, such as rebalancing only every two years. For many investors, implementing an annual rebalancing is optimal.
Hade varit intressant att höra hur @Lysa resonerat när de kommit fram till sina gränser för ombalansering!?
2 gillningar
Jag tror inte man bör titta på tid när man ombalanserar, utan snarare volatilitet.
Tittar man på tid kan man annars missa viktiga rörelser.
T.ex om vi hade Amundi i portföljen innan covid slog till och ombalanserade 1:e jan 2020 och sedan väntade ett år så hade vi missat väldigt viktig ombalansering under tiden.
5 gillningar
Ping @Zino något bra ställe där man kan se historisk standardavvikelse per fond/tillgångsslag?
1 gillning
Nordnet för vanliga fonder, JustETF för ETF:er.
1 gillning
Effekten Av Månatliga Insättningar: 2x Hävstång
I en tidigare post simulerade jag effekten av månatliga insättningar, där vi såg att våra månatliga insättningar kan hjälpa oss att dämpa nedgångar, minska urholkningseffekten och öka den geometriska snittavkastningen.
Vad händer då om vi tar det ett steg längre och investerar i en ETF med 2x daglig hävstång?
Vi investerar $10,000 i denna ETF 1:e Jan 2008 (i början av finanskrisen), gör sedan insättningar på $1000 varje månad och håller till 1:e Jan 2014.
Vi jämför också med att investera i SP500 utan hävstång.
(Valde en kort simuleringsperiod här eftersom jag tänker att 100% aktier med 2x daglig hävstång bara skulle vara en vettig strategi under ett antal år, när ens månatliga insättningar fortfarande kan hjälpa till att dämpa nedgångar).
Intressanta resultat!
SP500 hade utan hävstång och utan påverkan av månatliga insättningar en årlig avkastning på 6.13% TWRR (Time-Weighted Rate of Return) och en största nedgång på -48%.
Med påverkan av månatliga insättningar hade en SP500 årlig avkastning på 14.09% MWRR (Money-Weighted Rate of Return) och en största nedgång på -13%. Inte illa!
Våran 2x ETF hade utan påverkan av månatliga insättningar en årlig avkastning på 6.69% TWRR och en största nedgång på -77% (ouch).
Med påverkan av månatliga insättningar ökade årliga avkastningen till 24.84% MWRR (!!) med en största nedgång på -44%.
Där kan vi snacka positiv effekt!
Slutsats: 100% aktier med 2x daglig hävstång må inte vara något för folk som är nära “stay rich”-fasen, men är man i början av sin sparkarriär och gör månatliga insättningar så skulle det faktiskt kunna vara en vettig strategi, om man har rätta psyket, då det största problemet med dessa ETF:er vanligtvis annars är den stora urholkningseffekten, men med månatliga insättningar så blir det mycket bättre.
4 gillningar
Ja folk hänger upp sig på 1x leverage av någon anledning. Ingen magi med just 1x, någon kanske bara klarar av 0.8x exponering och någon mer. Läste att 2x var någon slags max innan marginalnyttan avtog och urholkningen blev orimligt stor.
2 gillningar
Tack för den intressanta jämförelsen!
Ett problem med hävstång är, förutom “volatility drag”, är att den kostar. I Nordnet 125 motsvarar denna räntan på de ytterligare 25 % som är marknadsexponerade.
Vilken ETF med 2x daglig hävstång använde du i din jämförelse, och hur hög är kostnaden för hävstången?
1 gillning
Xact 2 bull kostar 0.6% år + rullning (redovisas väl under transaktionskostnader?) av terminen.
Finns motsvarande ETFer för S&P500 och dax.
Har man en lite större portfölj men inte gigantisk kan det enklaste vara att bara ligga med terminen och rulla varje månad.
Det var mina spontana tankar.
1 gillning
Det var en artificiellt simulerad ETF. Jag la till en räntekostnad på 3%.
Jag såg att short term treasuries hade en avkastning på 2.25% under denna period, så jag bara testade 3%. Ingen djup tanke bakom det.
För S&P500 finns t.ex: Xtrackers S&P 500 2x Leveraged Daily Swap
Sedan 2010 har den haft en total avkastning på 1500% och iShares Core S&P500 har haft en avkastning på 440%.
3 gillningar
Hej @GetOut,
Tack för ditt tålamod till ett svar!
Här kommer ett svar som vi bland annat skrivit på vår Lysa Community på Facebook tidigare, men låt oss bli lite utförligare.
På Lysa finns det två typer av ombalanseringar - dels i målfördelningen mellan aktier och räntor, men även av de underliggande innehaven. Låt oss gå igenom båda:
Om du investerar i den breda (eller hållbara) portföljen kommer du att investera i tre Lysafonder - två aktiefonder (global och Sverige) och en räntefond. Dessa fonder utgör kundens målfördelning. Om det uppstår en avvikelse i den faktiska målfördelningen med ± 3 procentenheter under 5 bankdagar kommer det automatiskt att ske om ombalansering där ena delen säljs av för att köpa mer av det andra. Vi har valt en gräns på 3 procentenheter och en period på 5 bankdagar för ombalansering för att undvika för frekventa justeringar baserat på kortsiktiga dagliga börsrörelser, samtidigt som vi inte väntar för länge. Detta säkerställer att din portfölj behåller en lämplig risknivå både på kort och lång sikt. Se avsnitt: 2e, i vårt Whitepaper om Övervaka, ombalansera och uppdatera kundens portfölj. Dagar och procentenheter framgår inte men ovan är förklaringen. Länk: https://lysa.se/whitepaper
Ponera att du har 100 % aktier i bred fokus, då är du investerad i två fonder - Lysa Aktier C (global fond) till 80 % och 20 % i Lysa Sweden Equity Broad (Sverigefond). Om den globala fonden skulle gå väldigt bra medan om den svenska fonden går mindre bra uppstår en avvikelse enligt ovan och då kommer andelar säljas från den globala fonden för att köpa Sverigefonden. Det gör att fördelningen återgår till 80 % globalt och 20 % mot Sverige.
Underliggande innehav i respektive fond balanseras däremot dagligen i samband med att köp- och säljordrar läggs. Vi har en viss portföljsammansättning vi utgår från och varje order läggs på ett sådant vis att den procentuella målfördelningen mellan de olika innehaven bibehålls. Detta gör också att större avvikelser från önskad sammansättning inte hinner uppstå för de underliggande innehaven.
Ha en trevlig tisdag och vecka!
Bästa hälsningar,
Team Lysa
2 gillningar
Intressant att i Lysas exempel rebalaserar de antingen en gång i veckan eller dagligen.
Det är upp till var och en att avgöra hur “magiskt” det är.
Rikatillsammans rebalansderar årligen, det stämmer mer med mina erfarenheter och kunskaper.
Det är lika “magiskt” som så kallad dollar cost averaging (som de flesta här på forumet är negativa till).
Korslänkar till ett inlägg som egentligen hade passat bättre i denna tråd, för att lättare hitta inlägget i framtiden:
6 gillningar
Jag har hittat en väldigt bra artikel som förklarar ombalanseringspremien på ett intuitivt sätt, jag tror inte den har dykt upp här i tråden/forumet tidigare. Länk längre ner, jag ger mina tankar/insikter först och hoppas att fler läser den för att komma med egna tolkningar.
Ombalanseringspremien är resultatet av två olika mekanismer:
-
diversifiering som förbättrar geometrisk (verklig) avkastning pga minskad volatility drag (som man åstadkommer mha okorrelerade högvolatila komponenter)
-
högre geometrisk avkastning än buy-and-hold strategi pga automatisk sälj dyrt/köp billigt
För den första punkten är det enkelt att se att ombalanseringspremien inte bara består av skillnaden mellan aritmetisk och geometrisk avkastning: tar vi min allvädersportfölj från [tråd] så har vi 5,84% volatilitet som ger en volatility drag på 0,17%, medans den totala premien enligt formel är 1%.
Formeln (som beskrevs redan 1992 av Fama och Booth) är:
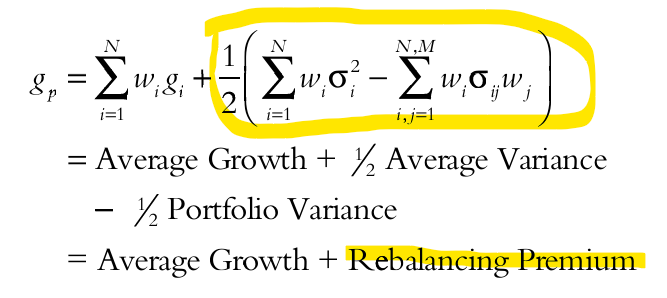
Premien är alltid positiv eftersom portföljens volatilitet alltid är lägre en den viktade medelvolatiteten för de olika tillgångarna när korrelationerna är mindre än 1.
Det här med hävstång (se längst ner) tas inte upp i artikeln, men jag tror mig förstå/se på formeln i det här formatet och det jag har fått med mina egna uträkningar, är hur det kan komma sig att hävstång kan öka premien på sådant sätt att Sharpekvoten faktiskt ökar:
Hävstången ökar volatiliteten (kvadratiskt) så att det finns mer “volatilitet att skörda”. Dock ökar samtidigt volatility drag kvadratiskt. Men om vi kan göra den negativa termen i premien tillräckligt liten, mha så okorrelerade tillgångar som möjligt, så kommer ombalanseringspremien att öka snabbare än volatility drag.
Det här låter ju lite för bra för att vara sant, att vi får högre absolut avkastning till lägre risk (eller kanske mer realistiskt samma risk om vi drar bort räntan för hävstången), så någon får gärna utmana denna tes 
Artikeln
Volatility Harvesting_JWM_Fall_2012.pdf (snifferquant.com)
Några utvalda stycken:
The excess return from volatility harvesting is not an expected arithmetic excess return derived from forecasting skill, security selection, or an informational advantage. Rather, it is the excess compounded return generated from rebalancing volatile assets over multiple time periods. This excess growth is available in liquid markets with assets that have volatilities greater than zero and correlations less than one.
We show that roughly half of the excess return from volatility harvesting comes from a diversification benefit and half from rebalancing.
Exhibit 2 shows the pattern of cumulative excess return from rebalancing by taking the ratio of portfolio values through time. Values above one indicate that a rebalancing portfolio is outperforming a buy and hold. The first four years fall below one, indicating under- performance. However, over the whole sample, the rebalanced portfolio had two times the growth Of the buy—and—hold portfolio. The trend of outperformance by the rebalancing strategy is predicted with remarkable accuracy by a rebalancing premium formula represented by the dashed line (see Equation in Appendix). In some periods, the rebalancing premium is less than theory predicts, and other times, it is greater.
This equation has been described as the “diversification return” by Booth and Fama [1992] and the “rebalancing premium” by Stein, Nemtchinov, and Pittman [2009]. Willenbrock [2011] observes that if diversification is the only “free lunch” of investing, then the diversification return from rebalancing is the only “free dessert.” Indeed, rebalancing is closely linked to diversification.
Manufacturing return out of thin air seems too good to be true. Where do these extra returns come from? There are two distinct components, which we validate empirically in the next section: extra return from diversification and extra return from rebalancing. The diversification return is due to reweighting the portfolio’s long-term exposures. For example, an equal- weighted portfolio has less weight in large-cap stocks and more weight in small—cap stocks than the market—cap index. Thus, it has a natural small-cap bias. If small-cap stocks outperform, then an equal—weighted strategy will benefit. However, in addition to creating long-term exposures, another way to earn return is through a pat- tern of trading. If you can consistently buy low and sell high, you can create positive portfolio growth, even if the overall asset growth is flat.
Intuitively, it is easy to see that trending hurts a rebalancing strategy and large reversals help. Rebalancing, however, id not merely related to momentum and reversal. A deeper reason exists for the observed outperformance. The coin-flipping thought experiment points this out. In that scenario, there is no concept of momentum or reversal since there is no serial correlation between the returns. The probability distribution at each point in time is identical and independent from what has occurred in the past. However, there is still “mean reversion” in this example. If 10 tails in a row are flipped, the mean return is -50%. The sample mean will “revert” to the long-term average as more flips are made. Even in this simple case of no serial correlation, the rebalancing premium is evident. In the more complex case using actual returns, there may be time dependencies. If asset prices experience “boom” periods followed by “bust” periods, then rebalancing will be even more valuable than theory predicts.
The key idea is that the growth of a portfolio is the weighted—average growth of the securities plus a rebalancing premium. This premium is always positive because the portfolio variance is always lower than the weighted-average variance of the individual assets when correlations are less than one. Higher volatility and lower correlation among the assets will lead to a higher rebalancing premium. Another interesting insight to be gained from this formula is that concentrated portfolios will produce a smaller rebalancing premium. For example, if the fixed weights are 99% and 1%, then the rebalancing premium will be lower because only a small portion of the portfolio is being rebalanced. The shape of the plot in Exhibit 1 reveals this result. The most diverse portfolio, equal weight, is not always the highest growth, but it is often close to the highest growth (Platen and Rendek [2010]). Portfolios with more assets and more evenly distributed weights should garner a higher benefit from rebalancing.
Övrigt: Hävstång på ombalanseringpremien (via ChatGPT):
The extension to include leverage is not always explicitly presented in textbooks but can be derived from the principles of leveraged portfolios. The key idea is that leverage magnifies both expected returns and the volatility of the assets by the square of the leverage factor. Thus, the rebalancing premium is also amplified by L^2 where L is the leverage factor.
7 gillningar
Jag har verifierat att grundformeln från ChatGPT är samma som den i artikeln i senaste inlägget, bara i en annan form (korrelationer vs covarians etc).
På hög nivå är formeln förvånansvärt enkel:
x = innehavens viktade snittvarians
y = portföljens volatility drag (portföljens varians delat med 2)
----
premie = x - y
Av detta ser man att porföljen blir belönad av höga enskilda varianser (hög volatilitet) i första termen samt av låg totalvarians i andra termen, som åstadkoms av okorrelerade komponenter.
Den sistnämnda termen får mig att fundera på om premien ska adderas till aritmetisk avkastning eller geometrisk 
För att vara konservativ, och så som jag har räknat i exemplet i allväderstråden, så räknar jag tills vidare att att den ska adderas till geometrisk, vilket i praktiken innebär att totalavkastningen “straffas” två gånger av volatility drag.
EDIT: hade skrivit fel i formeln, justerar/förenklar samtidigt.
3 gillningar