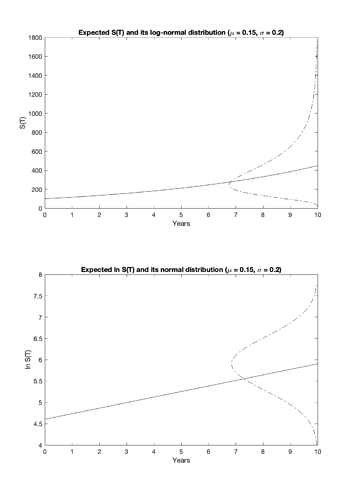
Intressant diskussion! Jag ska erkänna att jag inte heller läst precis hela tråden, men jag fastnade för några av illustrationerna över riskspridning över tid. Jag tror att det här är ett område där den förenklade bilden av att avkastningar är “normalfördelade” kan ge en lite felaktig bild. Typiskt modelleras avkastning med normalfördelade logaritmiska avkastningar, vilket över korta tidsperioder även ger mer eller mindre normalfördelade enkla/aritmetiska avkastningar. Över längre tid, eller med högre avkastningar, blir det dock ganska stor skillnad. Jag tog lite hjälp från ChatGPT att ta fram en figur över hur samma underliggande modell kan skilja väldigt mycket om vi vill titta på dess fördelning i log-skala eller med “vanlig” skala.
Vet inte riktigt hur man ställer sig till länkar för andra poddar så , men i senaste The memo av Howard Marks så pratar han om detta.
Vet inte om jag är tvåa på bollen dock och det va det som utlöste funderingarna kring risk med tanke på att figuren länkas i början av tråden.
Kan du ge oss höjdpunkterna från poddavsnittet med Howard Marks? ![]()
Det klassiska memot om Risk skrev han annars 2006 (sjukt att man kan det i huvudet).
Han använde sig av en tennis analogi för att förklara hur han ser på risk och vad man bör fundera över när man investerar beroende på vem man är. Man kan säga att man delar upp det i två olika sorters tennis beroende på vilket fall som gäller.
-
Två personer möts i en match, typ på den lokala tennisklubben. I den matchen handlar det om vem som är bäst defensiv, då man kan låta den andra göra misstag för att vinna matchen. Index-investeringar ser han som defensiva investeringar då man inte under/över presterar utan får precis det marknaden ger vilket är det “perfekta defensiva spelet”.
-
I den andra matchen är det två proffs som spelar. Där måste man istället lyckas slå bollar som den andra inte lyckas ta (alltså spela offensivt, och lyckas med det) då man inte kan förlita sig på den andras misstag. Men proffsen är trots allt inte lika bra. Den ena har flera grand-slam och inte den andra. Alltså måste den sämre spelaren slå bollar som ligger över sin egentliga kompetensnivå för att lyckas vinna, “spela bättre än sig själv” (alltså ha tur/en bra dag). Så trots att man är bland de bästa i världen och ska tävla med den bästa måste man ha tur för att vinna.
Då det är få som skulle satsa på den lokala tennisstjärnan om den skulle möte t.ex. Nadal i en match, men det säger inte att den lokala tennisstjärnan inte kan vinna en boll genom att ha tur.
Småsparare bör därför fokusera på att spela defensivt (investera i index) och inte ge sig i kast med att vinna över de som är proffs då man trotts allt spelar två olika sorters spel trots att man kallar det samma sak.
Känner att jag inte riktigt gör analogin rättvisa, utan det va något mer välformulerat när han pratade om det.
Vem vet?
Jag snubblar omkring och har ingen kristallkula.
Att utgå från att historisk nettoavkastning, dvs massa % utöver den galopperande tillgångsinflationen, fortsätter som framtida är kanske väl optimistiskt.
Gränsande till naivt att ha sådan riskaptit.
Utgå från korrigerade tillgångspriser under lång tid, i synnerhet på små marknader som den svenska.
Med ett korrigerat ränteläge till snart sunda nivåer runt 8% över lång tid ändras spelets regler.
Artikel på ämnet som jag hittade idag:
In 1962, economist Paul Samuelson showed that when using standard economic assumptions, time diversification is a mathematical fallacy. In other words, the idea that investors should hold relatively safe assets for near-term goals while funding their long-term goals with riskier assets is false. Per Samuelson, if you have liked stocks for 40 years, you should like them equally well for one month.
och
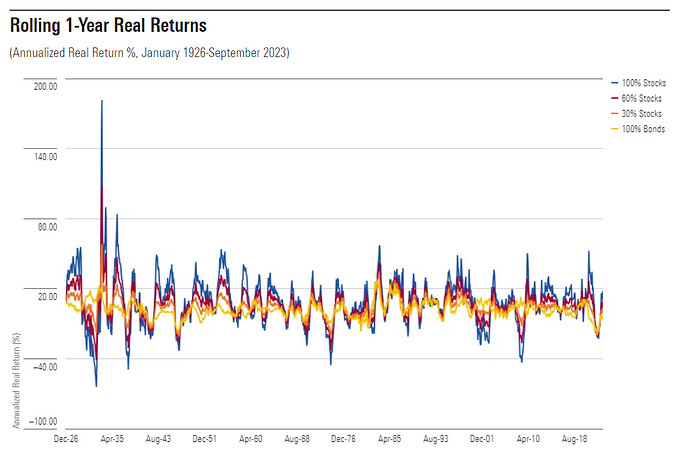
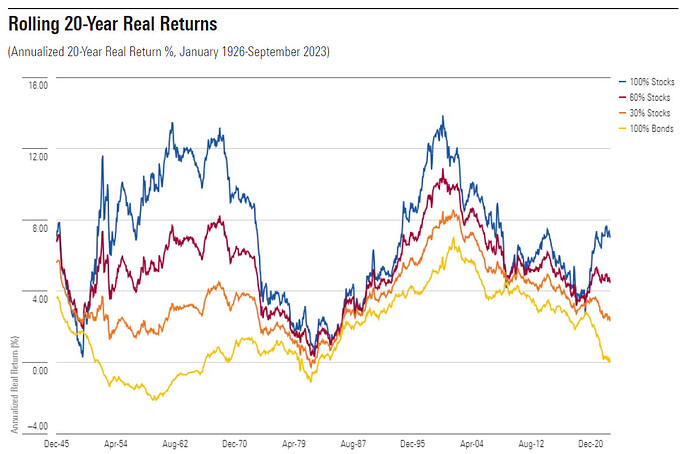
This column contains four charts. Each portrays the same information over periods of different lengths. They show since January 1926 the after-inflation returns for four portfolios: 1) 100% U.S. large-company stocks, 2) 60% stocks and 40% intermediate-term U.S. government bonds, 3) 30% stocks and 70% bonds, and 4) 100% bonds. The first picture, which depicts one-year results, looks familiar.
Here are the summary statistics. The table shows how frequently the 100% stock portfolio beat each of the other three portfolios. It also indicates how often each investment suffered a double-digit loss (again, the returns are in real terms).
1-Year Summary
Portfolio Stocks Winning % Against Double-Digit Loss %(Annual) 100% Stocks n/a 17% 60% Stocks 67% 9% 30% Stocks 67% 5% 100% Bonds 66% 3%
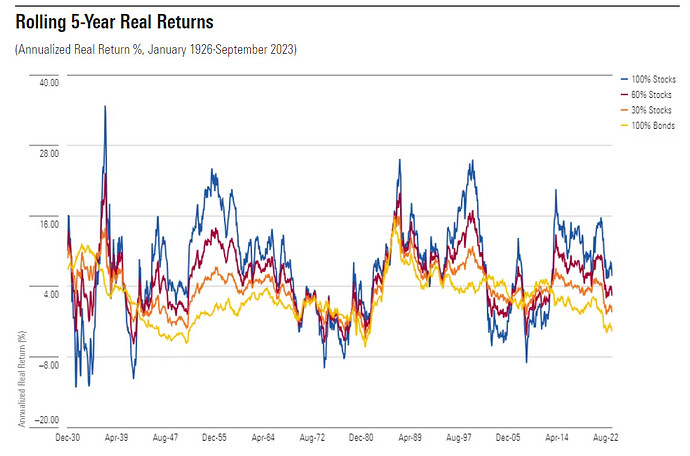
5 års sparhorisont
5-Year Summary
Portfolio Stocks Winning % Against Double-Digit Loss %(Cumulative) 100% Stocks n/a 16% 60% Stocks 72% 16% 30% Stocks 73% 5% 100% Bonds 75% 13%
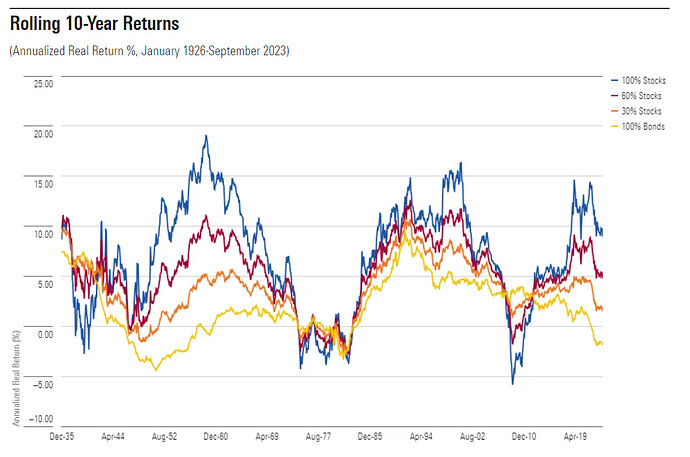
10 års sparhorisont
10-Year Summary
Portfolio Stocks Winning % Against Double-Digit Loss %(Cumulative) 100% Stocks n/a 10% 60% Stocks 78% 6% 30% Stocks 81% 4% 100% Bonds 83% 17%
20 års sparhorisont
20-Year Summary
Portfolio Stocks Winning % Against Double-Digit Loss % (Cumulative) 100% Stocks n/a 0% 60% Stocks 93% 0% 30% Stocks 97% 0% 100% Bonds 99% 19%
At 20 years, the risk evaluation is reversed. Bonds are the true danger, routinely realizing double-digit losses, after inflation is considered. The safe path comes from equities. Placing 30% of the portfolio into stocks eliminates cumulative losses exceeding 10%, although on a few occasions, the 30% stocks portfolio did shed purchasing power over 20 years. When stocks make up either 60% or the entire portfolio, however, the losses disappear. In none of the historic 20-year rolling periods did either the balanced or the 100% stocks portfolio land in the red. They always gained at least something .
Samt den uppföljande artikeln:
Last week’s “How Time Horizon Affects the Odds of Equity Investing” mentioned that while stocks are widely regarded as prudent for long-term shareholders but speculative for short-term owners, Nobel Laureate Paul Samuelson disagreed. In two articles written in the 1960s, Samuelson maintained that if investors like equities for three decades, they should like them equally well for three months. His claim refutes the popular concept of time diversification, which is that holding risky assets becomes safer with the passage of time.
Unusually, Samuelson’s claim is both undisputed and ignored. That combination is striking, as the other major academic discoveries from that time—Harry Markowitz’s Modern Portfolio Theory, William Sharpe’s capital asset pricing model, and Eugene Fama’s efficient-market hypothesis—have become deeply embedded in common investment practice. Yet Samuelson’s insight languishes. Nobody invests that way—not retail shareholders, not financial advisors, not institutional investors.
Jag saknar lite begränsningar i resonemangen för att det ska gå att använda praktiskt.
Tidsrymd. Liv?
Konfidensintervall. Korta svansarna på normfördelningsklockorna i era skisser. Evigheten är oändlig.
Signifikansnivå. t.ex på resonemanget att förlora allt i en diversifierad portfölj eller global indexfond. Tror att man med säkerhet (99%) kan säga att det inte kommer hända under en livstid. Risken finns men den är inte signifikant.
Så, borde inte risken minska med tiden om man har ett konfidensintervall på 99% på hur mycket portföljen varierar. De vill säga, om den maximalt, inom intervallet, negativa utvecklingen en viss tid (5-10år) fortfarande håller ett högre värde jämfört med ett sparande i sparkonto (samma spahorisont och insättningar). Så bör man spara på detta sätt, aktier/fonder.
Rätta mig om jag resonerar tokigt ![]()
Att säga att en viss aktie skulle vara lägre risk beroende på att du äger den länge är lite som att säga att det är mindre sannolikhet att slå en sexa med en tärning om du precis dessförinnan slagit en sexa. Sannolikheten är alltid 1/6 att slå 1-6 som bekant.
Jag roade mig någon gång för länge sedan att se till totalavkastningen på NYSE absurt långt tillbaka i tiden, över 100 år vill jag minnas, och roade mig bland annat med att studera hur stor andel av åren som hade dåliga utfall dels sett till alla år, men även hur många treårsperioder, femårsperioder, sjuårsperioder och tioårsperioder som var trista/dåliga utfall. Inte helt oväntat så minskade sannolikheten för “trista utfall” (dålig real avkastning) ju längre tidsperiod, men att uppåt 10 års horisont så började sannolikheten för trista utfall närma sig andelen år med trista utfall under samtliga åren (80-120 år har jag för mig). Detta fick mig tidigt att dra slutsatsen att aktier inte är något man ska investera pengar i som man behöver inom 8-10 år, snarare än 3-5 år som många idag ger uttryck för. Men det är givetvis inte investeringens risk som förändras över tid, investeringen (aktien) vet nämligen inte om att du äger den. Det är din risk (sannolikhet) för “trista utfall” som historiskt/empiriskt förändras om du äger S&P500-indexfond 12 år istället för 3 år.
Kanske är det för att jag således bara investerar “långa pengar” i aktier som jag känner mig väldigt bekväm i riskerna med att investera i princip 100% av långa pengar i dem. Jag kan inte påstå att det bekommit mig nämnvärt att en av mina två depåer är ner med 1/3 senaste två åren, det har ingen praktiskt betydelse för mig. Fortsatta köp blir till lägre värderingar vilket säkert visar sig vara bra om 10-20 år, men inte heller detta bekommer mig så mycket i dagsläget. Den aktuella depån är explicit tillskapad för att generera hög totalavkastning på lång sikt - utan större hänsyn till volatilitet. Standardavvikelsen ligger väl i nivå med OMXS30, och något därutöver i trängre lägen (som 2022-2023), men temat på depån har under en längre serie år gett i snitt >16% per år. Varför klaga?
Ja vi pratar om risk som om det vore en egen enhet. I tärningsfallet ovan borde enheten vara sannolikhet per tärningskast. Analogt mot investeringar borde enheten kunna beskrivas som risk per tidsenhet(eller risk per omsatt volym). Med tärningar vet vi att sannolikhet per kast ej ändras med antalet kast. Hur är det då inom investeringar? Pest, krig, rapportdagar, myndighetsbeslut, stor eller liten marknad, ändrar dessa risken per tidsenhet eller är den konstant? Optionsmarknaden indikerar att risk per tidsenhet fluktuerar över tid och att då jämnar tid ut risk. @janbolmeson nu när du fått 109 inputs har du fått någon ny insyn i orginalfrågan?
En tanke som slog mig i efter det senaste avsnittet, handlar inte risken egentligen bara om hur flexibel man är med när man behöver betala utgifter och inte om att ha en fast spar/tidshorisont?
Med tanke på att risken för nedgång i en global aktieindexfond nästkommande dag varje enskild dag är ca46%, enligt bilden @janbolmeson hade i sin presentation här Risk: det viktigaste att veta för dig som sparar i indexfonder (inkl. 20+ grafer) 📈 | 343. Bör man ju ha 54% att om man kan skjuta utgiften en dag ha mer pengar att spendera. Alltså kommer flexibilitet att göra att man nästan kan strunta i risken man tar givet att man har en tillräckligt bra riskjusterad avkastning.
Tänker då på flexibilitet inte enbart utifrån konsumtion utan det är även giltigt om man t.ex. belånar portföljen för att öka den förväntade avkastningen där man får stående utgifter för ränta osv. Samt att kreditkort, buffert, mellanriskhinken etc kommer att öka flexibiliteten i ekonomin.
Lite förenklat; Kan jag skjuta min utgift på framtiden 1 dag? Då har jag med 54% sannolikhet mer pengar efter den dagens slut.
Man bör därför kanske vända på frågan och tänka när jag har XXX kronor investerat kan jag köpa Y sak istället för när det gått XXX tid kan jag köpa Y sak?
Snyggt tänkt. ![]()
Ja, jag tänker med alla diskussioner kring uttag och FIRE att "flexbilitet" verkar vara det absolut viktigaste samt att som @Jonathan.S beskriver i sin risk-tråd: “Vad är risken att jag inte kan leva det livet som jag kan leva”
Det är så jag tänker här:
Jag tänker att det finns en poäng med att ha pengarna i investeringen så länge som möjligt i genomsnitt, även om det inte är i en obruten sekvens.
Längre tidshorisont ökar antalet tillfällen da man kan sälja med vinst.
Risken är mer eller mindre konstant sasom sadan sett utifran varje given tidpunkt under den tid som kapitalet förblir investerat.
Lite som jag ser det.
Hade helt missat den tråden/inlägget och jag tror det va precis samma tanke som precis slog mig. Man borde alltså sträva efter försök att öka flexibiliteten kring när utgifterna kommer för att kunna bära en större risk i sina investeringar och därmed få en högre avkastning.
Jag gillar förslagen kring hur man kan öka sin flexibilitet också. Jag tror att man oftast kan vara mer flexibel än vad man ser vid första anblick kring t.ex. husköp, bil, semester etc.
Om pengarna inte räcker till resan man drömt om, kan man välja ett annat resmål? Kan man resa en kortare tid? Välja ett billigare hotell eller ett b&b? Hitta ett ressätt som tar längre tid men är billigare?
Återkommer i att vi säger att t.ex. Stockholmsbörsen brukar avkasta 8 % med en standardavvikelse på ca 22%. Dvs att ca 68% av utfallen hamnar i intervallet -14% till +30% ett enskilt år och med ca 95% sannolikhet inom -36% och +50%.
Här kan väl någon riktigt mattekunnig jämföra med ränta och sätta in i Kelly kriteriet och få fram hur många % man bör satsa per tidsenhet.
A detailed paper by Edward O. Thorp and a co-author estimates Kelly fraction to be 117% for the American stock market SP500 index. [14] Significant downside tail-risk for equity markets is another reason [15] to reduce Kelly fraction from naive estimate (for instance, to reduce to half-Kelly).
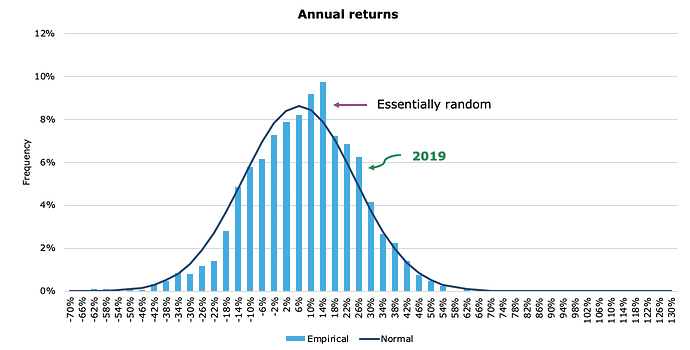
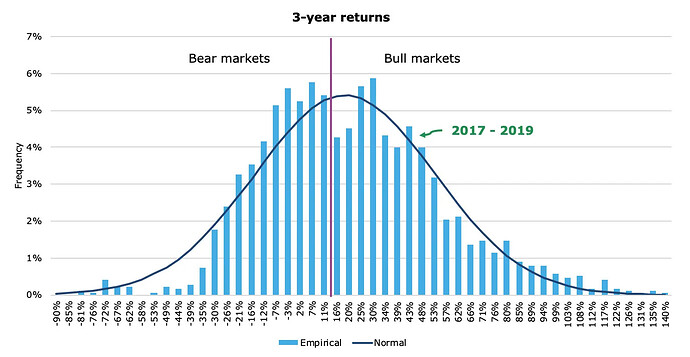
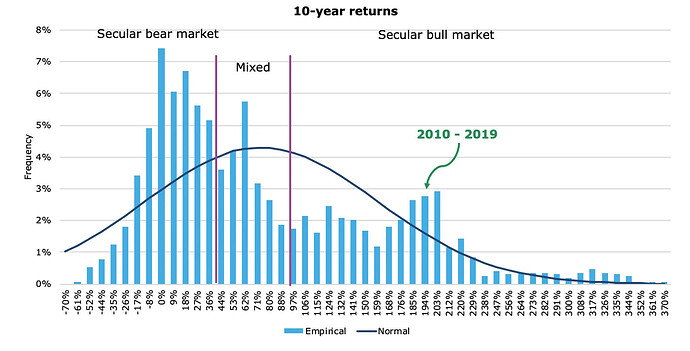
Hittade några intressanta grafer som visar att fördelningen inte ändras helt intuitivt vid förlängning av sparhorisonten:
Källa: The distribution of stock market returns
Självklart var det ju redan gjort, 117% Såfan också.
Ingen jävla feg half-Kelly där inte.