Då är jag med på hur du räknar. Så aktier har alltså inte en årlig avkastning på 7% över riskfria räntan utan 5.88% enligt dig?
Ja, i jämförelse mellan aktier, räntefonder och bankkonto så är aspekten volatilitetsförlust viktig att ta hänsyn till, dels för att
-
det påverkar enskilda tillgångsslag negativt
-
samt att man kan, med rätt kombination av tillgångsslag, motverka det
Den sistnämnda punkten innebär bl.a att man inte bara kan vikta och summera ihop olika tillgångsslags avkastning.
Enligt mig? ![]() Nejdå, jag har inte kommit på det själv :
Nejdå, jag har inte kommit på det själv :
Volatility tax - Wikipedia
Guide to Volatility Drag for Financial Advisors
Även om storleken varierat ganska ordentligt så har som synes arrangemanget hitintills givit ett positivt ekonomiskt bidrag under perioder när räntan varit stabil (2019-2021), uppåtgående (2022-2023) och nedåtgående (2024).
Diffen förändras kontinuerligt i takt med att min sammanlagda sparränta och/eller låneränta ändras. Skulle jag t ex idag omvandla hela mitt bolån till rörlig ränta skulle det positiva ekonomiska bidraget minska till 1%.
(Edit: Skulle jag idag dessutom omvandla även hela mitt banksparande till rörlig ränta skulle det positiva ekonomiska bidraget minska ytterligare, till 0,6%.)
Men är inte denna effekt redan inräknad om man räknar på en avkastning på aktier? Dvs. om man håller 100% aktier under en längre tid, säg 30 år, kan jag då räkna med en avkastning på ca 7% per år eller 5.88% per år utöver riskfria räntan?
CAGR = [(Slutvärde / Startvärde) ^ (1 / Antal år)] – 1
Det finns ingen standardavvikelse eller volatilitetsförlust i formeln för att räkna ut CAGR.
Som jag förstått det så innebär riskpremie = aritmetisk avkastning, dvs att man inte tar hänsyn till volatilitet.
För en långsiktig investering så behöver man definitivt ta hänsyn till det:
(Ska du räkna ut historisk/verkligt CAGR så behöver du såklart inte känna till något annat än start- och slutvärde. )
Så om vi antar att avkastningen för aktier över riskfri ränta är: 5.63%
5.88% minus avgift på 0.25% (ungefär vad en global indexfond hamnar på)
Avkastningen för räntor ser jag inte i dina beräkningar? Jag antar 0.88% just nu (1%-0.12% avgift). Antar att din standardavvikelse kommer dra ner avkastningen här också? Att räkna med en given korrelation här introducerar ännu en osäkerhetsfaktor men en korrelation på 0.1 är väl ändå en högre korrelation mot aktier än bankkonto har?
Antag avkastningen för bankkonto är 0% över riskfri ränta. Detta går att påverka ganska lätt genom att byta bank eller binda kapitalet i t.ex 3 månader eller ett år, vilket blir extra relevant om man ska ha bankkonto under längre tid. Så det är ganska lätt att få upp bankkonto över den riskfria räntan enligt min åsikt.
Så om vi räknar igen med ovan antaganden:
70 % aktier + 30 % bank = 0.7 * 5.63 + 0.3 * 0 = 3,941 %
60 % aktier + 40 % räntor = 0.6 * 5.63 + 0.4 * 0.88 = 3,73%
Kan du redovisa hur du kom fram till 4.3% CAGR? Vart kommer den extra avkastningen ifrån som jag inte har med i beräkningen ovan? Är det “ombalanseringseffekten”? Vad har du räknat med för “ombalanseringseffekt” för bankkonto respektive räntor och korrelation i så fall? Jag antar att bankkonto har en korrelation på 0 mot alla andra tillgångar eftersom den är helt okorrelerad men det kanske finns en matematisk uträkning för detta någonstans också? Hur ofta räknar du med att ombalanseringen sker för att uppnå denna “ombalanseringseffekt”? En gång per dag som Lysa har eller en gång per år som många gör när de gör manuella ombalanseringar? Eller ombalanserar du vid en givet delta mot ursprungfördelningen?
Detta är en annan diskussion, men spontant menar jag att binda räntan är en form av risk i sig, vilket innebär att det inte är riskfri ränta längre.
Du måste räkna ut den geometriska avkastningen för portföljen som helhet, det går inte att ta de enskilda komponenterna för sig. Så, för hela portföljen:
- räkna ut den aritmetiska avkastningen mha riskpremie
- räkna ut standardavvikelse (baserat på vikter och korrelationer)
- vilken man kan använda för att räkna ut volatilitetsförlusten
- och på så sätt vet man vad den geometriska avkastningen blir
- ombalanseringspremien är portföljens genomsnittsvarians minus volatilitetsförlust (så man gynnas alltså av volatilitet i de enskilda tillgångarna så länge de är okorrelerade med varann).
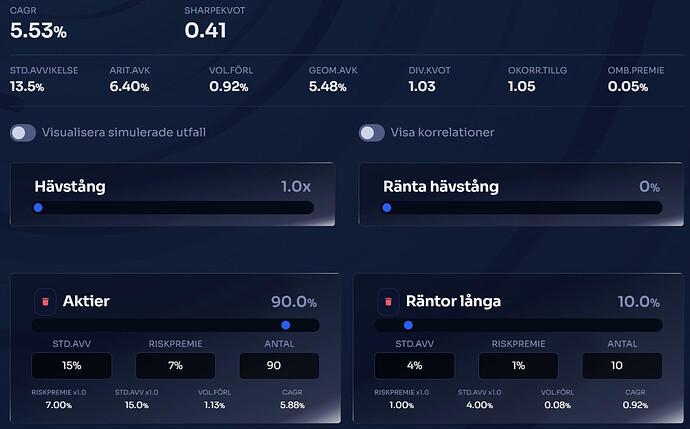
Jag har inte tid (iaf inte nu) att skriva ut alla uträkningar då jag inte räknar manuellt utan kör mitt eget program för att räkna ut det… jag klipper in skärmdumpar längst ner där alla värden framgår:
Formeln är baserad på att man ombalanserar löpande, men troligtvis spelar det inte en avgörande roll då man istället “fångar trender” om man ombalanserar mer sällan (Finns mycket om detta i Ombalanseringens magi).
OBS: jag ska undersöka mer hur man ska tänka kring real kontra nominell avkastning vid dessa uträkningar.
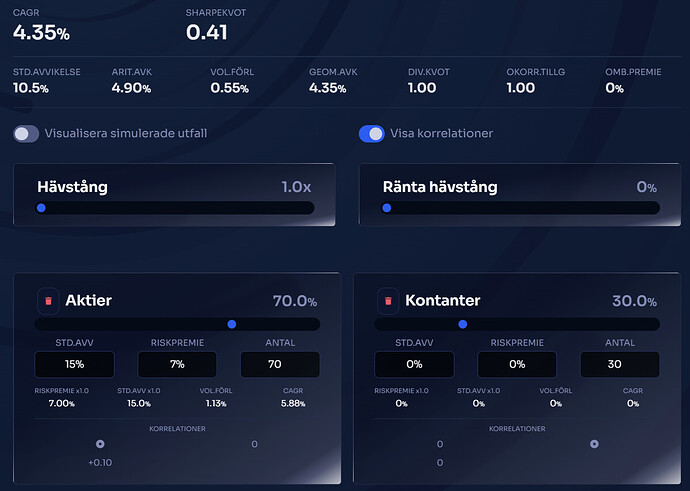
70/30 aktier/riskfri ränta:
Not: noll ombalanseringspremie
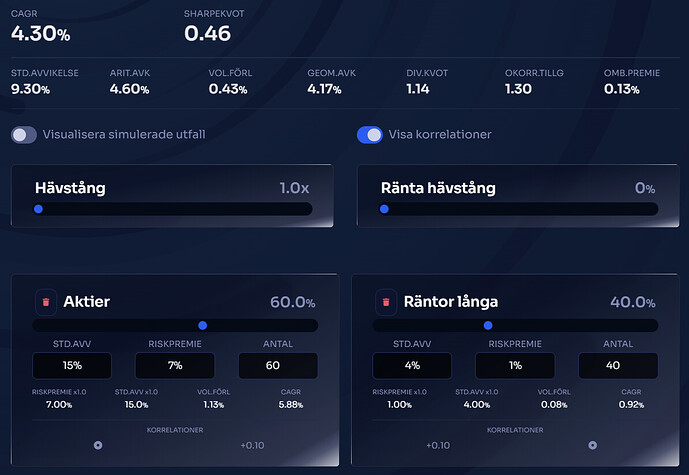
60/40 aktier/räntefond
Not: En liten ombalanseringspremie, högre sharpekvot pga lägre standardavvikelse
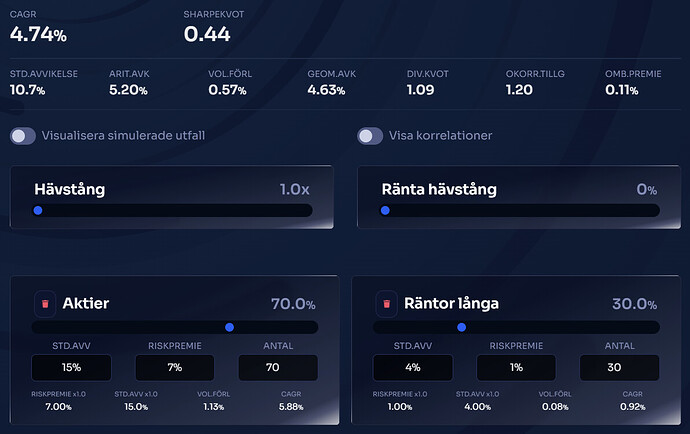
70/30 aktier/räntefond
Not: Nästan samma totala standardavvikelse som översta fallet trots 4% volatilitet hos räntor mot 0% hos kontanter, pga okorrelation
90/10 aktier/räntefond
Not: först här är vi (nere) på samma sharpekvot som 70/30 kontanter
Fast ju oftare man ombalanserar, desto större blir vissa svansrisker. Exempelvis förlorade gissningsvis den som hade en 50/50-portfölj i 20-talets Tyskland runt 50% av portföljen utan ombalansering och närmare 100% av portföljen vid kontinuerlig ombalansering.
Håller med. Men frågan var om bankkonto är rimligt på lång sikt. På lång sikt är det ju fullt rimligt att binda pengarna under en tidsperiod och få en ökning av räntan. Min bedömning är att det går att få rörlig sparränta med ungefär samma ränta som bolån. Binder man på 3 mån brukar räntan öka med ca 0.5% och på 1 år ca 0.75% även om det inte stämmer i tider med sjunkande ränta. Så bankkonto kan ge högre avkastning än räntor med denna approach.
Om man ombalanserar årligen bör väl standardavvikelsen beräknas på årsbasis och om man ombalanserar dagligen så bör väl standardavvikelsen beräknas på dagsbasis? Standardavvikelsen på års basis bör väl rimligen vara lägre än på dagsbasis?
Angående dina beräkningar:
-
Du ser inte ut att ha räknat med någon avgift på varken aktier eller räntor?
-
Även i dina beräkningar så är ju CAGR högre för 70/30 aktier/bankkonto än 60/40 aktier/räntor. Detta utan att räkna med att man kan binda bankkonto eller avgift för räntor.
-
Jag är lite tveksam till ombalanseringspremien för bankkonto. Om korrelationen är 0 så är den ju “bättre” än för räntor som är 0.1? Då borde väl bankkonto ha en högre ombalanseringspremie? Jag får en känsla av att ditt program räknar fel här. Även om avkastningen är 0% över inflationen så kan det ju vara så att aktier avkastar -50% ett år och bankkontot +5% (om den riskfria räntan är 5%) och då kan man ombalansera och få en ombalanseringspremie även där?
Vid ex-ante beräkningar så brukar man bortse (eller inkludera dom i schablonavkastningen) från kostnader och fokusera på den teoretiska avkastningen i förhållande till den risk man tar.
Ja (0.05% högre), men som jag skrev så är den riskjusterade avkastningen högre för aktier/räntor.
Jag föreslår att du läser ombalanseringens magi eller googlar, jag sitter inte på någon hemlig information som inte redan tillgänglig ![]()
Jag avslutar med en prompt från ChatGPT:
Can you get a rebalancing premium using an asset with zero volatility?
No, you cannot achieve a rebalancing premium using an asset with zero volatility, because the rebalancing premium relies on the interaction of volatility and correlation between assets in a portfolio. Here’s why:
What is the Rebalancing Premium?
The rebalancing premium arises from the process of periodically rebalancing a portfolio back to fixed weights. It is the extra return generated due to:
- Volatility: Fluctuations in asset prices allow rebalancing to buy low and sell high.
- Low or Negative Correlation: Assets with low or negative correlation create opportunities for this rebalancing mechanism to add value.
Why Zero Volatility Doesn’t Work
An asset with zero volatility (e.g., cash or a risk-free bond) does not fluctuate in value, which means:
- No Volatility Interaction: The zero-volatility asset contributes nothing to creating price differentials that enable “buy low, sell high” during rebalancing.
- No Variance to Capture: If one asset is perfectly stable, the portfolio volatility is solely determined by the volatile asset(s). Rebalancing only adds a premium when multiple assets have variances that interact.
Mathematical Perspective
Consider a two-asset portfolio:
- Asset A: Volatile, with expected return μA\mu_AμA and volatility σA\sigma_AσA.
- Asset B: Zero-volatility, with a fixed return RBR_BRB.
Since Asset B contributes no variance or covariance, the rebalancing opportunities depend entirely on Asset A’s movements. However, rebalancing cannot generate additional returns because there are no interactions or diversification effects between the assets.
Real-World Implication
A rebalancing premium requires:
- At least two volatile assets, where price movements create opportunities.
- Low or negative correlation between the assets to maximize variance reduction during rebalancing.
Using an asset with zero volatility (e.g., cash) does not directly contribute to the rebalancing premium but can serve other purposes, such as reducing overall portfolio risk or acting as a liquidity reserve.
Ok, då är jag med på hur du räknar och varför du har den uppfattning du har.
Så låt oss prata om elefanten i rummet, avkastningen för bankkonto. Jag hävdar att avkastningen för bankkonto är högre än den riskfria räntan.
Just nu:
Styrränta: 2.75% (=den riskfria räntan enligt mig).
Bolåneränta 3 mån: 3.42% (Enligt sbab: https://www.sbab.se/1/privat/vara_rantor.html#!/kalkyl#%2Frantor)
Ränta 3 mån: 3,85% (Marginalen, som är en bank jag haft över 10 år: Fasträntekonto - Öppna sparkonto med fast ränta | Marginalen)
Om man anstränger sig och håller på och flyttar runt kan man få högre: 4% på Hoist spar (Jämför sparformer - hoistspar.se)
Jag tror att alla anser att bolåneräntan är högre än den riskfria räntan eftersom låneutgivaren tar en risk? Bankkonto räntan är högre än bolåneräntan just nu → Slutsatsen bör därför vara att bankkonto räntan är högre än den riskfria räntan. Min uppfattning är att just nu är den bankkonto räntan 3.85 - 2.75 = 1.1% högre än riskfri ränta.
Ja, vi har kanske olika uppfattningar om vad som är “riskfri ränta”. För mig är det precis vad det heter - den högsta ränta jag kan få utan att ta någon risk, ex. sparkonto (fria uttag, ingen bindningstid, insättningsgaranti).
Men det väsentliga i denna del av diskussionen är ju hur man brukar definera riskpremie, är det “över styrräntan”, eller är det över den “i praktiken tillgängliga riskfria räntan”, dvs sparkonto.
Vi pratar om medellånga räntor som ex. AMF Lång/Mix. Jämför man de mot sparkontoräntor de senaste 10-20 åren så kan man se vilka antaganden man göra om ev. diff i avkastning. Har såna räntefonder någon förväntad riskpremie i förhållande till sparkonto? Min gissning är ja.
(Den andra delen av diskussionen var ju ombalanseringspremie, och där är det bara räntefonder som gäller pga att sparkonto saknar volatilitet)
Min gissning är nej så då är det inte så konstigt vi har olika utgångspunkt. Kollar jag på vad AMF räntefond lång innehåller:
Så verkar huvuddelen vara räntepapper utgivna av svenska staten. Kollar man på vad dessa papper har för ränta:
As of the latest update on 14 Dec 2024 15:23 GMT+0, the Sweden 5 Years Government Bond has a yield of 1.960% . This yield represents the annual return that investors can expect to receive if they hold the bond until its maturity in 5 Years.
Så ser jag inte hur man kan anta att den skulle avkasta högre än sparkonto 3 månader (3.85% ränta).
Utöver detta är det en risk att göra antagandet att historisk korrelation kommer gälla i framtiden eller när aktier kraschar. Bankkonto däremot kan man lita på att det ger sin bestämda avkastning.
Jämför man med US t bills däremot så blir det ju en annan historia:
3 Month Treasury Bill Rate is at 4.23%
Nej, det är sant.
I en annan tråd (Dags för räntefond? - Nr 6 av JFB) blev det en sidodiskussion om termen riskfri ränta, men jag tror detta är en bättre plats för en praktisk följdfråga.
@RobertK och @Ateist_investor, ni berättade att ni tänker på riskfri ränta utifrån räntenivån på obundet sparkonto med insättningsgaranti (istället för t ex RB:s styrränta eller 3 mån SSVX).
Min fråga är vilken/vilka datakälla ni två - eller någon annan för den delen - använder för att få grepp om denna variabels (räntenivån på obundet sparkonto med insättningsgaranti) utveckling historiskt? Har själv ännu inte lyckats hitta någon bra datakälla som sträcker sig bakåt och helst ger data på månadsbasis.
Nja, jag investerar med i bästa fall napkin math. Har ingen datakälla, men lägger likvida pengar på Avanzas bästa rörliga partner konto, så jag jämför således med det. Orkar inte flytta deg till andra banker pga jag vill inte vänta på nån strulig nischbanks havererade site eller dyl.
Jag använder också “napkin math” men min känsla är att bankkonto räntan är ungefär lika med boräntan för SBAB (just nu ca 3.22% men bankräntan är just nu 3.85% för den bank jag använder). Det har varierat lite över tiderna men de brukar följas åt rätt bra är min erfarenhet.
Däremot om boräntan på SBAB = “riskfria räntan” är en helt annan diskussion.
EDIT:
Upptäckte nu att räntan på avanzas partners: Avanza är 2.55% just nu, dvs hela 1.3% lägre än vad jag får på mitt vanliga sparkonto (som jag haft i 10+ år som tidigare nämnts utan att flytta runt.) 2.55% låter rimligt att den “riskfria räntan” skulle ligga på i min mening och då har Marginalen 3 månader 1.3% ränta över riskfri ränta. Detta skulle rimma väl med att AMF räntefond lång har 1% över riskfri och skulle således ha en lägre avkastning än mitt vanliga bankkonto.
Jag höll på att skriva ett inlägg relaterat till just detta i denna tråd, men postade aldrig då det kändes lite off-topic. Så det passade bra att du ställde frågan här istället!
En viktig sak att påpeka är att begreppet riskfri ränta fungerar ganska dåligt just i svensk kontext.
Tittar vi på USA är spridningen relativt liten mellan amerikanska statspapper (3-månads T-bill 4,34%), och högsta sparkontoränta (upp till 5%). Så riskfri ränta ≈ sparkontoränta.
Tittar vi på Sverige är däremot spridningen relativt stor mellan svenska statspapper (3-månads stadsskuldväxel 2,29%) och högsta rörliga sparkontoränta (upp till 4%). Tittar vi på svenska korta räntefonder ligger AMF Kort fn på 3,07% i förväntad avkastning, och AMF Företagsobligation på 3,69% (taget från AMFs hemsida). Så riskfri ränta ≠ sparkontoränta.
Varför är räntan på svenska sparkonton så mycket högre än svenska statspapper och räntefonder just nu?
- Marknaden för svenska statspapper är inte helt effektiv (många påtvingade aktörer på liten marknad)
- Stor skillnad i styrränta mellan Sverige och USA (nischbankerna kan utnyttja detta genom FX-carry, dvs köpa utländska räntepapper för inlånade pengar)
- Historiskt låg kreditspread (väldigt lite betalt för kreditrisk just nu)
- Inverterad räntekurva (inget betalt alls för ränterisk just nu)
Punkt 2-4 är tillfälligheter som gör att sparkonton är väldigt svårslagna just nu, vilket inte är normalfallet. Apropå punkt 2 hade det verkligen varit intressant att se hur mycket FX-carry och valutarisk nischbankerna exponerar sig mot, men som vi slipper oroa oss över tack vare insättningsgarantin.
Beträffande din fråga om historisk utveckling för sparkonto vs styrränta och räntefond rekommenderar jag denna tråd, om du inte sett den.
Jag tror inte det är en större faktor. Jag snabbkollade årsredovisningar på Marginalen, Norion, TF och Resurs, och skuldsidan med inlåning från allmänheten var höftat till 95% speglad i utlåning till allmänheten och sen resterande 5% i statsskuldsförbindelser och obligationer.
Vi får se hur lång tid det dröjer innan “normalfallet” återkommer då. Jag hade pengar i en isländsk bank 2008 med runt 6% ränta som skyddades av svenska insättningsgarantin. Banken gick mycket riktigt i konkurs och jag fick tillbaka alla pengarna. Detta är 16 år sedan.